题目内容
9. 设椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$(a>b>0)的左、右焦点分别为F1,F2,上顶点为A,过点A与AF2垂直的直线交x轴负半轴于点Q,且$2\overrightarrow{{F_1}{F_2}}+\overrightarrow{{F_2}Q}$=$\overrightarrow 0$.
设椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$(a>b>0)的左、右焦点分别为F1,F2,上顶点为A,过点A与AF2垂直的直线交x轴负半轴于点Q,且$2\overrightarrow{{F_1}{F_2}}+\overrightarrow{{F_2}Q}$=$\overrightarrow 0$.(Ⅰ)求椭圆C的离心率;
(Ⅱ)若过A,Q,F2三点的圆恰好与直线$\sqrt{7}$x-y+$\sqrt{7}$+$4\sqrt{2}$=0相切,求椭圆C的方程;
(Ⅲ)过F2的直线L与(Ⅱ)中椭圆C交于不同的两点M、N,则△F1MN的内切圆的面积是否存 在最大值?若存在,求出这个最大值及此时的直线方程;若不存在,请说明理由.
分析 (Ⅰ)由题意可知:$\overrightarrow{AQ}$=(-3c,-b),$\overrightarrow{A{F_2}}$=(c,-b),由$\overrightarrow{AQ}$⊥$\overrightarrow{A{F_2}}$,即$\overrightarrow{AQ}$•$\overrightarrow{A{F_2}}$=-3c2+b2=0,a2=4c2,e=$\frac{c}{a}=\frac{1}{2}$;
(Ⅱ)由$\frac{{|{-\sqrt{7}c+\sqrt{7}+4\sqrt{2}}|}}{{\sqrt{7+1}}}$=2c,解得c=1则a=2,b=$\sqrt{3}$,即可求得椭圆的标准方程;
(Ⅲ)由要使△F1MN内切圆的面积最大,只需R最大,此时${S_△}_{F_1}{\;}_{MN}$也最大,设直线l的方程为x=my+1,代入椭圆方程,由韦达定理,弦长公式及三角形的面积公式可知${S_△}_{F_1}{\;}_{MN}$=|y1-y2|=$\frac{{12\sqrt{{m^2}+1}}}{{3{m^2}+4}}$,t=$\sqrt{{m^2}+1}$,则t≥1,${S_△}_{F_1}{\;}_{MN}$=$\frac{12t}{{3{t^2}+1}}=\frac{12}{{3t+\frac{1}{t}}}$(t≥1),由函数的单调性可知:当t=1时,${S_△}_{F_1}{\;}_{MN}$=4R有最大值3,即可求得m的值,求得直线方程.
解答 解:(Ⅰ)依题意A(0,b),F1为QF2的中点.
设F1(-c,0),F2(c,0),则Q(-3c,0),$\overrightarrow{AQ}$=(-3c,-b),$\overrightarrow{A{F_2}}$=(c,-b),
由$\overrightarrow{AQ}$⊥$\overrightarrow{A{F_2}}$,即$\overrightarrow{AQ}$•$\overrightarrow{A{F_2}}$=-3c2+b2=0,∴-3c2+(a2-c2)=0,
即a2=4c2,
∴e=$\frac{c}{a}=\frac{1}{2}$.(3分)
(Ⅱ)由题Rt△QAF2外接圆圆心为斜边QF2的中点,
F1(-c,0),半径r=2c,
∵由题Rt△QAF2外接圆与直线$\sqrt{7}x-y$+$\sqrt{7}$+$4\sqrt{2}$=0相切,
∴d=r,即$\frac{{|{-\sqrt{7}c+\sqrt{7}+4\sqrt{2}}|}}{{\sqrt{7+1}}}$=2c,解得c=1.
∴a=2,c=1,b=$\sqrt{3}$.
所求椭圆C的方程为:$\frac{x^2}{4}+\frac{y^2}{3}=1$(6分)
(Ⅲ)设M(x1,y1),N(x2,y2)由题知y1,y2异号,
设△F1MN的内切圆的半径为R,则△F1MN的周长为4a=8,
∴${S_△}_{F_1}{\;}_{MN}$=$\frac{1}{2}$(|MN|+|F1M|+|F1N|)R=4R,
∴要使△F1MN内切圆的面积最大,只需R最大,此时${S_△}_{F_1}{\;}_{MN}$也最大.(8分)
${S_△}_{F_1}{\;}_{MN}$=$\frac{1}{2}$|F1F2|.|y1-y2|=|y1-y2|,
由题知,直线l的斜率不为零,可设直线l的方程为x=my+1,
由$\left\{\begin{array}{l}x=my+1\\ \frac{x^2}{4}+\frac{y^2}{3}=1.\end{array}\right.$,得(3m2+4)y2+6my-9=0,
由韦达定理,得y1+y2=$\frac{-6m}{{3{m^2}+4}}$,y1y2=$\frac{-9}{{3{m^2}+4}}$,(△>0⇒m∈R)
${S_△}_{F_1}{\;}_{MN}$=|y1-y2|=$\sqrt{{{(y{\;}_1+{y_2})}^2}-4{y_1}{y_2}}$=$\frac{{12\sqrt{{m^2}+1}}}{{3{m^2}+4}}$.
令t=$\sqrt{{m^2}+1}$,则t≥1,${S_△}_{F_1}{\;}_{MN}$=$\frac{12t}{{3{t^2}+1}}=\frac{12}{{3t+\frac{1}{t}}}$(t≥1),
当t=1时,${S_△}_{F_1}{\;}_{MN}$=4R有最大值3.
此时,m=0,Rmax=$\frac{3}{4}$.
故△F1MN的内切圆的面积最大值为$\frac{9π}{16,}$
此时直线l的方程为x=1.(12分)
点评 本题考查椭圆的标准方程及简单几何性质,考查直线与椭圆的位置关系,韦达定理,弦长公式及三角形的面积公式,考查椭圆与函数的单调性及最值综合应用,考查计算能力,属于中档题.

| A. | sin$\frac{1}{2}$<cos$\frac{1}{2}$<tan$\frac{1}{2}$ | B. | cos$\frac{1}{2}$<sin$\frac{1}{2}$<tan$\frac{1}{2}$ | ||
| C. | sin$\frac{1}{2}$<tan$\frac{1}{2}$<cos$\frac{1}{2}$ | D. | tan$\frac{1}{2}$<sin$\frac{1}{2}$<cos$\frac{1}{2}$ |
| A. | 1或2 | B. | 2 | C. | 1 | D. | 1或-2 |
| A. | 命题“若a>b,则ac>bc”是真命题 | |
| B. | 命题“若a2+b2=0,则a,b全为0”是真命题 | |
| C. | 命题“若a=0,则ab=0”的否命题是“若a≠0,则ab≠0” | |
| D. | 命题“若a=0,则ab=0”的逆否命题是“若ab≠0,则a≠0” |
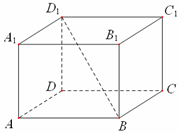 如图,在正四棱柱ABCD-A1B1C1D1中,底面ABCD的边长为7,BD1与底面所成角的大小为$arctan\frac{6}{7}$,则该正四棱柱的高等于$6\sqrt{2}$.
如图,在正四棱柱ABCD-A1B1C1D1中,底面ABCD的边长为7,BD1与底面所成角的大小为$arctan\frac{6}{7}$,则该正四棱柱的高等于$6\sqrt{2}$. 如图所示的多面体中,ABCD是菱形,BDEF是矩形,ED⊥平面ABCD,∠BAD=$\frac{π}{3}$,AD=2,DE=$\sqrt{3}$.
如图所示的多面体中,ABCD是菱形,BDEF是矩形,ED⊥平面ABCD,∠BAD=$\frac{π}{3}$,AD=2,DE=$\sqrt{3}$.