题目内容
19. 如图所示的多面体中,ABCD是菱形,BDEF是矩形,ED⊥平面ABCD,∠BAD=$\frac{π}{3}$,AD=2,DE=$\sqrt{3}$.
如图所示的多面体中,ABCD是菱形,BDEF是矩形,ED⊥平面ABCD,∠BAD=$\frac{π}{3}$,AD=2,DE=$\sqrt{3}$.(Ⅰ)异面直线AE与DC所成的角余弦值;
(Ⅱ)求证平面AEF⊥平面CEF;
(Ⅲ)在线段AB取一点N,当二面角N-EF-C的大小为60°时,求|AN|.
分析 (Ⅰ)由AB∥DC,知∠BAE就是异面直线AE与DC所成的角,由此能求出异面直线AE与DC所成的角余弦值.
(Ⅱ)取EF的中点M,推导出∠AMC是二面角A-EF-C的平面角,由此能证明平面AEF⊥平面CEF.
(Ⅲ)建立空间直角坐标系,利用向量法能求出结果.
解答 解:(Ⅰ)∵AB∥DC,
∴∠BAE就是异面直线AE与DC所成的角,
连接BE,在△ABE中,$AB=2,AE=\sqrt{7}=BE$,
∴$cos∠BAE=\frac{7+4-7}{{2×2×\sqrt{7}}}=\frac{{\sqrt{7}}}{7}$,
∴异面直线AE与DC所成的角余弦值为$\frac{{\sqrt{7}}}{7}$.…(4分)
证明:(Ⅱ)取EF的中点M.由于ED⊥面ABCD,ED∥FB,
∴ED⊥AD,ED⊥DC,FB⊥BC,FB⊥AB,
又ABCD是菱形,BDEF是矩形,∴△ADE,△EDC,△ABF,△BCF是全等三角形,
∴AE=AF,CE=CF,∴AM⊥EF,CM⊥EF,
∴∠AMC是二面角A-EF-C的平面角 …(6分)
由题意$AM=CM=\sqrt{6}$,$AC=2\sqrt{3}$,∴AM2+CM2=AC2,即AM⊥MC.
∴∠AMC=90°,∴平面AEF⊥平面CEF.…(8分)
解:(Ⅲ)建立如图的直角坐标系,由AD=2,
则M($\frac{\sqrt{3}}{2},\frac{1}{2},\sqrt{3}$),C(0,2,0),$A({\sqrt{3},1,\sqrt{3}})$,$E({0,0\sqrt{3}})$,$F({\sqrt{3},1,\sqrt{3}})$.
平面CEF的法向量$\overrightarrow{n_1}=\overrightarrow{AM}=({-\frac{{\sqrt{3}}}{2},\frac{3}{2},\sqrt{3}})$.(10分)
设$N({\sqrt{3},λ,0})$,则$\overrightarrow{EN}=({\sqrt{3},λ,-\sqrt{3}})$,$\overrightarrow{EF}=({\sqrt{3},1,0})$
设平面NEF的法向量$\overrightarrow{n_2}=({x,y,z})$,
则$\left\{{\begin{array}{l}{\overrightarrow{EF}•\overrightarrow{n_2}=0}\\{\overrightarrow{EN}•\overrightarrow{n_2}=0}\end{array}}\right.$,即$\left\{{\begin{array}{l}{\sqrt{3}x+y=0}\\{\sqrt{3}x+my-\sqrt{3}z=0}\end{array}}\right.$,令x=1,则$y=-\sqrt{3},z=1-λ$,得$\overrightarrow{n_2}=({1,-\sqrt{3},1-λ})$.(11分)
因为二面角N-EF-C的大小为60°,
所以$cos60°=\frac{{\overrightarrow{n_2}•\overrightarrow{AN}}}{{\overrightarrow{|{n_2}}|•|\overrightarrow{AN}|}}=\frac{{|-\frac{{\sqrt{3}}}{2}-\frac{{3\sqrt{3}}}{2}+\sqrt{3}({1-λ})|}}{{\sqrt{\frac{3}{4}+\frac{9}{4}+3}\sqrt{1+3+{{({1-λ})}^2}}}}$,…(12分)
整理得λ2+6λ-3=0,解得$λ=2\sqrt{3}-3$,…(13分)
所以$|AN|=2\sqrt{3}-2$…(14分)
点评 本题考查异面直线所成角的余弦值的求法,考查面面垂直的证明,考查满足条件的线段长的求法,是中档题,解题时要认真审题,注意空间思维能力的培养.

| A. | ?x∈(0,+∞),lnx≠x-1 | B. | ?x∉(0,+∞),lnx=x-1 | ||
| C. | ?x0∈(0,+∞),lnx0≠x0-1 | D. | ?x0∉(0,+∞),lnx0=x0-1 |
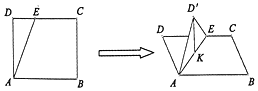 如图,在正方形ABCD中,AB=2,E为线段CD上一动点,现将△AED沿AE折起,使点D在面ABC上的射影K在直线AE上,当E从D运动到C,则点K所形成轨迹的长度为( )
如图,在正方形ABCD中,AB=2,E为线段CD上一动点,现将△AED沿AE折起,使点D在面ABC上的射影K在直线AE上,当E从D运动到C,则点K所形成轨迹的长度为( )| A. | $\sqrt{2}$ | B. | 2$\sqrt{2}$ | C. | $\frac{π}{2}$ | D. | $\frac{π}{4}$ |
 设椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$(a>b>0)的左、右焦点分别为F1,F2,上顶点为A,过点A与AF2垂直的直线交x轴负半轴于点Q,且$2\overrightarrow{{F_1}{F_2}}+\overrightarrow{{F_2}Q}$=$\overrightarrow 0$.
设椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$(a>b>0)的左、右焦点分别为F1,F2,上顶点为A,过点A与AF2垂直的直线交x轴负半轴于点Q,且$2\overrightarrow{{F_1}{F_2}}+\overrightarrow{{F_2}Q}$=$\overrightarrow 0$.