Question

4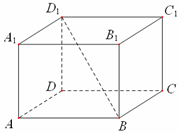．如图，在正四棱柱ABCD-A₁B₁C₁D₁中，底面ABCD的边长为7，BD₁与底面所成角的大小为$arctan\frac{6}{7}$，则该正四棱柱的高等于$6\sqrt{2}$．

Answer 1

分析 根据正四棱柱ABCD-A₁B₁C₁D₁的侧棱D₁D⊥底面ABCD，判断∠D₁BD为直线BD₁与底面ABCD所成的角，即可求出正四棱柱的高．

解答 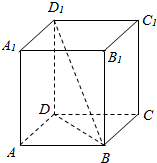解：∵正四棱柱ABCD-A₁B₁C₁D₁的侧棱D₁D⊥底面ABCD，
∴∠D₁BD为直线BD₁与底面ABCD所成的角，
∴tan∠D₁BD=$\frac{6}{7}$，
∵正四棱柱ABCD-A₁B₁C₁D₁中，底面ABCD的边长为3，
∴BD=7$\sqrt{2}$，
∴正四棱柱的高=7$\sqrt{2}×\frac{6}{7}$=$6\sqrt{2}$，
故答案为：$6\sqrt{2}$

点评 本题考查了正四棱柱的性质，正四棱柱的高的计算，考查了线面角的定义，关键是找到直线与平面所成的角．