题目内容
20.已知数列{an}通项公式为an=$\frac{1}{n(n+1)}$,其前m项和为$\frac{9}{10}$,则双曲线$\frac{x^2}{m+1}-\frac{y^2}{m}$=1的渐近线方程是( )| A. | y=±$\frac{9}{10}$x | B. | y=±$\frac{10}{9}$x | C. | y=±$\frac{{3\sqrt{10}}}{10}$x | D. | y=±$\frac{{\sqrt{10}}}{3}$x |
分析 利用数列求和,推出m,然后求解双曲线的渐近线方程.
解答 解:数列{an}通项公式为an=$\frac{1}{n(n+1)}$,其前m项和为$\frac{9}{10}$,
可得1-$\frac{1}{2}+\frac{1}{2}-\frac{1}{3}+\frac{1}{3}-\frac{1}{4}$$+…+\frac{1}{m}-\frac{1}{m+1}$=$\frac{9}{10}$,
即1-$\frac{1}{m+1}$=$\frac{9}{10}$.解得m=9.
双曲线$\frac{{x}^{2}}{10}-\frac{{y}^{2}}{9}$=1的渐近线方程:y=±$\frac{{3\sqrt{10}}}{10}$x.
故选:C.
点评 本题考查数列求和,双曲线的简单性质的应用,考查计算能力.

练习册系列答案
相关题目
11.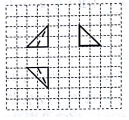 如图所示,网格纸上每个小格都是边长为1的正方形,粗线画出的是一个几何体的三视图,则该几何体的表面积为( )
如图所示,网格纸上每个小格都是边长为1的正方形,粗线画出的是一个几何体的三视图,则该几何体的表面积为( )
 如图所示,网格纸上每个小格都是边长为1的正方形,粗线画出的是一个几何体的三视图,则该几何体的表面积为( )
如图所示,网格纸上每个小格都是边长为1的正方形,粗线画出的是一个几何体的三视图,则该几何体的表面积为( )| A. | 2+2$\sqrt{3}$+$\sqrt{6}$ | B. | 4+2$\sqrt{3}$+$\sqrt{6}$ | C. | 4+4$\sqrt{3}$+$\sqrt{6}$ | D. | 2+$\sqrt{3}$+$\sqrt{6}$ |
15.函数f(x)=x3-3x2+1的单调递减区间是( )
| A. | (2,+∞) | B. | (-∞,2) | C. | (-∞,0) | D. | (0,2) |
5.椭圆$\frac{x^2}{16}+\frac{y^2}{4}=1$上的一点A关于原点的对称点为B,F为它的右焦点,若AF⊥BF,则△AFB的面积是( )

| A. | 2 | B. | 4 | C. | 1 | D. | $\frac{\sqrt{3}}{2}$ |
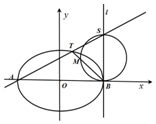 已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的长轴长为2$\sqrt{2}$,离心率为$\frac{\sqrt{2}}{2}$.
已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的长轴长为2$\sqrt{2}$,离心率为$\frac{\sqrt{2}}{2}$.