题目内容
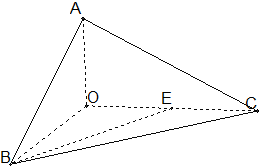如图，已知三棱锥O-ABC的侧棱OA，OB，OC两两垂直，且OA=1，OB=OC=2，E是OC的中点．（1）求O点到面ABC的距离；
（2）求异面直线BE与AC所成的角的余弦值；
（3）求二面角E-AB-C的余弦值．
考点：与二面角有关的立体几何综合题,异面直线及其所成的角
专题：空间位置关系与距离,空间角
分析：几何法：
（1）取BC的中点D，连AD、OD，过O点作OH⊥AD于H，由已知条件推导出OH的长就是所要求的距离．由此能求出O点到面ABC的距离．
（2）取OA的中点M，连EM、BM，则EM∥AC，∠BEM是异面直线BE与AC所成的角．由此能求出异面直线BE与AC所成的角的余弦值．
（3）连结CH并延长交AB于F，连结OF、EF．∠EFC就是所求二面角的平面角．由此能求出二面角E-AB-C的余弦值．
向量法：
（1）以O为原点，OB、OC、OA分别为x、y、z轴建立空间直角坐标系．利用向量法能求出点O到面ABC的距离．
（2）
=(2，-1，0)，
=(0，2，-1)，利用向量法能求出异面直线BE与AC所成的角的余弦值．
（3）分别求出平面EAB的法向量和平面ABC的法向量，利用向量法能求出二面角E-AB-C的余弦值．
（1）取BC的中点D，连AD、OD，过O点作OH⊥AD于H，由已知条件推导出OH的长就是所要求的距离．由此能求出O点到面ABC的距离．
（2）取OA的中点M，连EM、BM，则EM∥AC，∠BEM是异面直线BE与AC所成的角．由此能求出异面直线BE与AC所成的角的余弦值．
（3）连结CH并延长交AB于F，连结OF、EF．∠EFC就是所求二面角的平面角．由此能求出二面角E-AB-C的余弦值．
向量法：
（1）以O为原点，OB、OC、OA分别为x、y、z轴建立空间直角坐标系．利用向量法能求出点O到面ABC的距离．
（2）
| EB |
| AC |
（3）分别求出平面EAB的法向量和平面ABC的法向量，利用向量法能求出二面角E-AB-C的余弦值．
解答：
（本小题满分14分）
几何法：
解：（1）取BC的中点D，连AD、OD，
∵OB=OC，则OD⊥BC、AD⊥BC，
∴BC⊥面OAD．过O点作OH⊥AD于H，
则OH⊥面ABC，OH的长就是所要求的距离．
BC=2
，OD=
=
．
∵OA⊥OB、OA⊥OC，∴OA⊥面OBC，
则OA⊥OD.AD=
=
，
在直角三角形OAD中，有OH=
=
=
．…（4分）
（2）取OA的中点M，连EM、BM，则EM∥AC，
∠BEM是异面直线BE与AC所成的角．
∵OA=1，OB=OC=2，E是OC的中点，
∴EM=
AC=
，BE=
=
，
BM=
=
，
cos∠BEM=
=
，
∴异面直线BE与AC所成的角的余弦值是
．…（8分）
（3）连结CH并延长交AB于F，连结OF、EF．
∵OC⊥面OAB，∴OC⊥AB．又∵OH⊥面ABC，∴CF⊥AB，EF⊥AB，
则∠EFC就是所求二面角的平面角．
作EG⊥CF于G，则EG=
OH=
．
在直角三角形OAB中，OF=
=
，
在直角三角形OEF中，EF=
=
=
，
∴sin∠EFG=
=
=
．
∴cos∠EFG=
=
，
∴二面角E-AB-C的余弦值为
．…（14分）
向量法：
解：（1）以O为原点，OB、OC、OA分别为x、y、z轴建立空间直角坐标系．
则有A（0，0，1）、B（2，0，0）、C（0，2，0）、E（0，1，0）．
设平面ABC的法向量为
=(x，y，z)，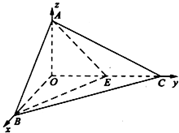
则由
⊥
知：
•
=2x-z=0；
由
⊥
知：
•
=2y-z=0．取
=(1，1，2)，
则点O到面ABC的距离为d=
=
=
．…（4分）
（2）
=(2，-1，0)，
=(0，2，-1)，
cos＜
，
＞=
=-
，
∴异面直线BE与AC所成的角的余弦值是
．…（8分）
（3）设平面EAB的法向量为
=(x，y，z)，
则由
⊥
知：
•
=2x-z=0；
由
⊥
知：
•
=2x-y=0．取
=(1，2，2)．
由（1）知平面ABC的法向量为
=(1，1，2)．
则cos＜
，
＞=
=
=
=
．
结合图形可知，二面角E-AB-C的余弦值为
．
∴二面角E-AB-C的余弦值为
．…（14分）
几何法：
解：（1）取BC的中点D，连AD、OD，
∵OB=OC，则OD⊥BC、AD⊥BC，
∴BC⊥面OAD．过O点作OH⊥AD于H，
则OH⊥面ABC，OH的长就是所要求的距离．
BC=2
| 2 |
| OC2-CD2 |
| 2 |
∵OA⊥OB、OA⊥OC，∴OA⊥面OBC，
则OA⊥OD.AD=
| OA2+OD2 |
| 3 |
在直角三角形OAD中，有OH=
| OA•OD |
| AD |
| ||
|
| ||
| 3 |
（2）取OA的中点M，连EM、BM，则EM∥AC，
∠BEM是异面直线BE与AC所成的角．
∵OA=1，OB=OC=2，E是OC的中点，
∴EM=
| 1 |
| 2 |
| ||
| 2 |
| OB2-OE2 |
| 5 |
BM=
| OM2+OB2 |
| ||
| 2 |
cos∠BEM=
| BE2+ME2-BM2 |
| 2BE•ME |
| 2 |
| 5 |
∴异面直线BE与AC所成的角的余弦值是
| 2 |
| 5 |
（3）连结CH并延长交AB于F，连结OF、EF．
∵OC⊥面OAB，∴OC⊥AB．又∵OH⊥面ABC，∴CF⊥AB，EF⊥AB，
则∠EFC就是所求二面角的平面角．
作EG⊥CF于G，则EG=
| 1 |
| 2 |
| ||
| 6 |
在直角三角形OAB中，OF=
| OA•OB |
| AB |
| 2 | ||
|
在直角三角形OEF中，EF=
| OE2+OF2 |
1+
|
| 3 | ||
|
∴sin∠EFG=
| EG |
| EF |
| ||||
|
| ||
| 18 |
∴cos∠EFG=
1-(
|
7
| ||
| 18 |
∴二面角E-AB-C的余弦值为
7
| ||
| 18 |
向量法：
解：（1）以O为原点，OB、OC、OA分别为x、y、z轴建立空间直角坐标系．
则有A（0，0，1）、B（2，0，0）、C（0，2，0）、E（0，1，0）．
设平面ABC的法向量为
| n1 |
则由
| n1 |
| AB |
| n1 |
| AB |
由
| n1 |
| AC |
| n1 |
| AC |
| n1 |
则点O到面ABC的距离为d=
|
| ||||
|
|
| 2 | ||
|
| ||
| 3 |
（2）
| EB |
| AC |
cos＜
| EB |
| AC |
| -2 | ||||
|
| 2 |
| 5 |
∴异面直线BE与AC所成的角的余弦值是
| 2 |
| 5 |
（3）设平面EAB的法向量为
| n |
则由
| n |
| AB |
| n |
| AB |
由
| n |
| EB |
| n |
| EB |
| n |
由（1）知平面ABC的法向量为
| n1 |
则cos＜
| n |
| n1 |
| ||||
|
|
| 1+2+4 | ||||
|
| 7 | ||
3
|
7
| ||
| 18 |
结合图形可知，二面角E-AB-C的余弦值为
7
| ||
| 18 |
∴二面角E-AB-C的余弦值为
7
| ||
| 18 |
点评：本题考查点到平面的距离的求法，考查异面直线所成的角的求法，考查二面角的余弦值的求法，解题时要认真审题，注意空间思维能力的培养．
练习册系列答案
阅读快车系列答案
相关题目
若a-b＜0，则下列各式中一定成立的是（ ）
| A、ac＜bc | ||||
| B、-a＞-b | ||||
C、
| ||||
| D、a2＜b2 |
A，B是焦点为F的抛物线y2=4x上的两动点，线段AB的中点M在直线x=t（t＞0）上．