题目内容
 有一海湾,海岸线近似为椭圆的一段弧NM,M、N为椭圆弧上两点,且MA⊥AB,NB⊥AB,AB间的距离为2公里,椭圆焦点为A、B,椭圆的短半轴长为
有一海湾,海岸线近似为椭圆的一段弧NM,M、N为椭圆弧上两点,且MA⊥AB,NB⊥AB,AB间的距离为2公里,椭圆焦点为A、B,椭圆的短半轴长为| 3 |
(1)求f(x)的表达式并求定义域;
(2)度假村P距离甲化工厂多少时,甲、乙两化工厂对度假村的废气污染程度和最小?
考点:函数的最值及其几何意义
专题:函数的性质及应用,导数的概念及应用
分析:(1)由点P在椭圆上,知|PA|+|PB|=4,设|PA|=x,则|PB|=4-x,由此可得P点受甲化工厂污染程度、受乙化工厂污染程度,即可求得污染程度和;
(2)令f(x)=
+
,求导函数,确定函数的单调性,从而可求函数的最小值.
(2)令f(x)=
| 8dmn |
| x2 |
| dmn |
| (4-x)2 |
解答:
解:(1)由点P在椭圆上,知|PA|+|PB|=4,设|PA|=x,则|PB|=4-x,
P点受甲油井污染程度为
,
P点受乙油井污染程度为
,
污染程度和为f(x)=
+
,定义域为[
,
]
(2)令f(x)=
+
=dmn(
+
),
求导函数,可得f′(x)=dmn(
+
)=-2dmn(
+
),
令f′(x)>0,解得x>
.
令f′(x)<0,解得x<
.
故x∈[
,
]时,函数为减函数;
当x=
时,f(x)取得最小值.
即度假村距离甲化工厂
km时,度假村的废气污染程度和最小.
P点受甲油井污染程度为
| 8dmn |
| x2 |
P点受乙油井污染程度为
| dmn |
| (4-x)2 |
污染程度和为f(x)=
| 8dmn |
| x2 |
| dmn |
| (4-x)2 |
| 3 |
| 2 |
| 5 |
| 2 |
(2)令f(x)=
| 8dmn |
| x2 |
| dmn |
| (4-x)2 |
| 8 |
| x2 |
| 1 |
| (4-x)2 |
求导函数,可得f′(x)=dmn(
| -16 |
| x3 |
| -2 |
| (4-x)3 |
| 8 |
| x3 |
| 1 |
| (4-x)3 |
令f′(x)>0,解得x>
| 8 |
| 3 |
令f′(x)<0,解得x<
| 8 |
| 3 |
故x∈[
| 3 |
| 2 |
| 5 |
| 2 |
当x=
| 5 |
| 2 |
即度假村距离甲化工厂
| 5 |
| 2 |
点评:本题考查导数的应用,考查函数思想,考查阅读能力、建模能力、运算能力.属于中档题.

练习册系列答案
相关题目

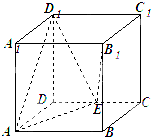 正方体ABCD-A1B1C1D1中,点E在棱CD上.
正方体ABCD-A1B1C1D1中,点E在棱CD上.