题目内容
已知函数f（x）=
（Ⅰ）求函数f（x）的单调递减区间；
（Ⅱ）求函数f（x）在区间[
，
]上的最大值和最小值．
| (cosx-sinx)sin2x |
| cosx |
（Ⅰ）求函数f（x）的单调递减区间；
（Ⅱ）求函数f（x）在区间[
| π |
| 24 |
| 11π |
| 24 |
考点：三角函数中的恒等变换应用,正弦函数的图象
专题：三角函数的图像与性质
分析：（Ⅰ）求出函数的定义域，化简函数的表达式，利用正弦函数的单调减区间求解函数的单调减区间即可．
（Ⅱ）通过x满足[
，
]求出相位的范围，利用正弦函数的值域，求解函数的最大值和最小值．
（Ⅱ）通过x满足[
| π |
| 24 |
| 11π |
| 24 |
解答：
（本小题满分14分）
解：f（x）的定义域为{x|x≠kπ+
，x∈R}k∈Z．k∈Z，f（x）=
=sin2x-2sin2x=
sin(2x+
)-1 …（4分）
（I）令2kπ+
≤2x+
≤2kπ+
π且x≠kπ+
，k∈Z解得，2kπ+
≤2x≤2kπ+
π，即 kπ+
≤x≤kπ+
π，x≠kπ+
，k∈Z
所以，f（x）的单调递减区间为[kπ+
，kπ+
)，(kπ+
，kπ+
]，k∈Z…（8分）
（II）由x∈[
，
]，可得2x+
∈[
，
]
当2x+
=
，即x=
时，f（x）max=f（
）=
-1．
当2x+
=
，即x=
时，f（x）min=f（
）=-
-1…（14分）
解：f（x）的定义域为{x|x≠kπ+
| π |
| 2 |
| (cosx-sinx)sin2x |
| cosx |
| 2 |
| π |
| 4 |
（I）令2kπ+
| π |
| 2 |
| π |
| 4 |
| 3 |
| 2 |
| π |
| 2 |
| π |
| 4 |
| 5 |
| 4 |
| π |
| 8 |
| 3 |
| 8 |
| π |
| 2 |
所以，f（x）的单调递减区间为[kπ+
| π |
| 8 |
| π |
| 2 |
| π |
| 2 |
| 5π |
| 8 |
（II）由x∈[
| π |
| 24 |
| 11π |
| 24 |
| π |
| 4 |
| π |
| 3 |
| 7π |
| 6 |
当2x+
| π |
| 4 |
| π |
| 2 |
| π |
| 8 |
| π |
| 8 |
| 2 |
当2x+
| π |
| 4 |
| 7π |
| 6 |
| 11π |
| 24 |
| 11π |
| 24 |
| ||
| 2 |
点评：本题考查三角函数的最值以及三角函数的化简与应用，两角和与差的三角函数的应用，考查计算能力．
练习册系列答案
培优好卷单元加期末卷系列答案
相关题目
函数y=
（x＞-1）图象的最低点坐标是（ ）
| x2+2x+5 |
| x+1 |
A、（1，2
| ||
| B、（0，2） | ||
C、（1，
| ||
| D、（1，4） |
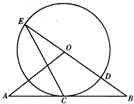如图，直线AB经过⊙O上一点C，且OA=OB，CA=CB，⊙O交直线OB于点E、D．
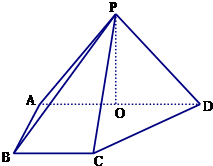如图，在四棱锥P-ABCD中，侧面PAD⊥底面ABCD，侧棱PA=PD=
如图，BC为圆O的直径，D为圆周上异于B、C的一点，AB垂直于圆O所在的平面，BE⊥AC于点E，BF⊥AD于点F．