题目内容
11.已知函数f(x)=|x2-1|+x2+kx.(1)对任意x∈[1,+∞),总有f(x)≥0成立,求实数k的取值范围;
(2)若-8<k<0,求函数|f(x)|在x∈[0,2]上的最大值.
分析 (1)由f(x)≥0分离出参数k,得k≥-2x+$\frac{1}{x}$,x∈[1,+∞),记g(x)=-2x+$\frac{1}{x}$,x∈[1,+∞),则问题等价于k≥g(x)max,由单调性可得g(x)max;
(2)对x和k进行分类讨论,结合二次函数的图象和性质,可得函数|f(x)|在x∈[0,2]上的最大值.
解答 解:(1)f(x)≥0⇒|x2-1|+x2+kx≥0⇒k≥-$\frac{|{x}^{2}-1|+{x}^{2}}{x}$=-2x+$\frac{1}{x}$,x∈[1,+∞),
记g(x)=-2x+$\frac{1}{x}$,易知g(x)在[1,+∞)上递减,
∴g(x)max=g(1)=-1,
∴k≥-1;
(2)当x∈[0,1)时,f(x)=|x2-1|+x2+kx=1-x2+x2+kx=kx+1,
由-8<k<0得:此时函数为减函数,当x=0时取最大值1,
当x∈[1,2]时,f(x)=|x2-1|+x2+kx=x2-1+x2+kx=2x2+kx-1,
此时函数的图象是开口朝上,且以直线x=$-\frac{k}{4}$∈(0,2)为对称轴的抛物线,
当$-\frac{k}{4}$∈(0,$\frac{3}{2}$],即-6≤k<0,函数f(x)x=2时,取最大值2k+7,
当$-\frac{k}{4}$∈($\frac{3}{2}$,2),即-8<k<-6,函数f(x)x=1时,取最大值k+1,
若-3<k<0,则2k+7>1,则函数|f(x)|在x∈[0,2]上的最大值为2k+7,
若-8<k≤-3,则2k+7≤1,则函数|f(x)|在x∈[0,2]上的最大值为1,
综上可得:函数|f(x)|在x∈[0,2]上的最大值为:$\left\{\begin{array}{l}2k+7,-3<k<0\\ 1,-8<k≤-3\end{array}\right.$
点评 本题考查的知识点是分段函数的应用,二次函数的图象和性质,难度中档.

| 数学 | 88 | 83 | 117 | 92 | 108 | 100 | 112 |
| 物理 | 94 | 91 | 108 | 96 | 104 | 101 | 106 |
(2)若该生的物理成绩达到115分,请你估计他的数学成绩大约是多少?
参考公式:$\stackrel{∧}{b}$=$\frac{\sum_{i-1}^{n}{x}_{i}{y}_{i}-n\overline{x}•\overline{y}}{\sum_{i=1}^{n}{x}_{i}^{2}-n(\overline{x})^{2}}$,$\stackrel{∧}{a}$=$\overline{y}$-$\stackrel{∧}{b}$$\overline{x}$
参考数据:$\sum_{i=1}^{n}{x}_{i}{y}_{i}$=70497,$\sum_{i=1}^{n}{x}_{i}^{2}$=70994.
 如图,在直三棱柱ABC-A1B1C1中,AC=3,BC=4,AB=5,AA1=4,点D是AB的中点.
如图,在直三棱柱ABC-A1B1C1中,AC=3,BC=4,AB=5,AA1=4,点D是AB的中点. 如图,在四棱锥P-ABCD中,底面ABCD为正方形,PA⊥底面ABCD,AB=AP,E为棱PD的中点.
如图,在四棱锥P-ABCD中,底面ABCD为正方形,PA⊥底面ABCD,AB=AP,E为棱PD的中点.
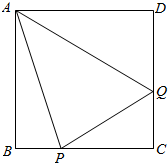 如图,某公司有一块边长为1百米的正方形空地ABCD,现要在正方形空地中规划一个三角形区域PAQ种植花草,其中P,Q分别为边BC,CD上的动点,∠PAQ=$\frac{π}{4}$,其它区域安装健身器材,设∠BAP为θ弧度.
如图,某公司有一块边长为1百米的正方形空地ABCD,现要在正方形空地中规划一个三角形区域PAQ种植花草,其中P,Q分别为边BC,CD上的动点,∠PAQ=$\frac{π}{4}$,其它区域安装健身器材,设∠BAP为θ弧度.