题目内容
6. 如图,在四棱锥P-ABCD中,底面ABCD为正方形,PA⊥底面ABCD,AB=AP,E为棱PD的中点.
如图,在四棱锥P-ABCD中,底面ABCD为正方形,PA⊥底面ABCD,AB=AP,E为棱PD的中点.(Ⅰ)证明:AE⊥CD;
(Ⅱ)求直线AE与平面PBD所成角的正弦值;
(Ⅲ)若F为AB中点,棱PC上是否存在一点M,使得FM⊥AC,若存在,
求出$\frac{PM}{MC}$的值,若不存在,说明理由.
分析 (Ⅰ)推导出PA⊥CD,AD⊥CD,从而CD⊥面PAD,由此能证明CD⊥AE.
(Ⅱ)以点A为原点建立空间直角坐标系,利用向量法能求出直线AE与平面PBD所成角的正弦值.
(Ⅲ)设$\overrightarrow{CM}=λ\overrightarrow{CP}\;,\;(0≤λ≤1)$,则 $\overrightarrow{FM}=\overrightarrow{FC}+\overrightarrow{CM}=(1-2λ,2-2λ,2λ)$.由此利用向量法能求出结果.
解答  (Ⅰ)证明:因为PA⊥底面ABCD,所以PA⊥CD.
(Ⅰ)证明:因为PA⊥底面ABCD,所以PA⊥CD.
因为AD⊥CD,AD∩AP=A,
所以CD⊥面PAD.
由于AE?面PAD,所以有CD⊥AE.…(4分)
(Ⅱ)解:依题意,以点A为原点建立空间直角坐标系(如图),
不妨设AB=AP=2,可得B(2,0,0),C(2,2,0),D(0,2,0),P(0,0,2).
由E为棱PD的中点,得E(0,1,1).$\overrightarrow{AE}$=(0,1,1)
向量$\overrightarrow{BD}=(-2,2,0)$,$\overrightarrow{PB}=(2,0,-2)$.
设$\overrightarrow n=(x,y,z)$为平面PBD的法向量,则$∫\overrightarrow{n}•\overrightarrow{BD}$=0,即∫-2x+2y=0.
不妨令y=1,可得$\overrightarrow{n}$=(1,1,1)为平面PBD的一个法向量.
设直线AE与平面PBD所成角为θ,
则sinθ=$\frac{|\overrightarrow{AE}•\overrightarrow{n}|}{|\overrightarrow{AE}|•|\overrightarrow{n}|}$=$\frac{2}{\sqrt{2}×\sqrt{3}}$=$\frac{\sqrt{6}}{3}$,
所以,直线AE与平面PBD所成角的正弦值为$\frac{{\sqrt{6}}}{3}$.…(11分)
(Ⅲ)解:向量$\overrightarrow{CP}=(-2,-2,2)$,$\overrightarrow{AC}=(2,2,0)$,$\overrightarrow{AB}=(2,0,0)$.
由点M在棱PC上,设$\overrightarrow{CM}=λ\overrightarrow{CP}\;,\;(0≤λ≤1)$.
故 $\overrightarrow{FM}=\overrightarrow{FC}+\overrightarrow{CM}=(1-2λ,2-2λ,2λ)$.
由FM⊥AC,得$\overrightarrow{FM}•\overrightarrow{AC}$=0,
因此,(1-2λ)×2+(2-2λ)×2=0,解得$λ=\frac{3}{4}$.
所以 $\frac{PM}{MC}=\frac{1}{3}$.…(13分)
点评 本题考查异面直线垂直的证明,考查线面角的正弦值的求法,考查两线段比值的求法,是中档题,解题时要认真审题,注意向量法的合理运用.

| A. | f(x1)<f(x2) | B. | f(x1)>f(x2) | C. | f(x1)=f(x2) | D. | 不确定 |
| A. | 若a≠0或b≠0,则a2+b2≠0 | B. | 若a2+b2≠0,则a≠0且b≠0 | ||
| C. | 若a2+b2≠0,则a≠0或b≠0 | D. | 若a=0且b=0,则a2+b2≠0 |
| A. | 三条交线中的任两条均为异面直线 | B. | 三条交线两两平行 | ||
| C. | 三条交线交于一点 | D. | 三条交线两两平行或交于一点 |
| A. | -3或2 | B. | 2 | C. | 3 | D. | -3 |
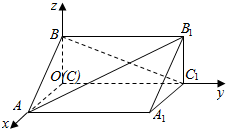 如图,在空间直角坐标系中有直三棱柱ABC-A1B1C1,CA=2CB,CC1=3CB,则直线BC1与直线AB1夹角的余弦值为( )
如图,在空间直角坐标系中有直三棱柱ABC-A1B1C1,CA=2CB,CC1=3CB,则直线BC1与直线AB1夹角的余弦值为( )| A. | $\frac{4\sqrt{35}}{35}$ | B. | $\frac{\sqrt{35}}{70}$ | C. | $\frac{2\sqrt{35}}{35}$ | D. | $\frac{2}{35}$ |
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |