题目内容
(Ⅰ) 已知数列{an}的前n项和Sn=-2n2+n-2,求{an}的通项公式.
(Ⅱ) 电脑的价格大约每3年下降
,那么今年花8100元买的一台电脑,9年后的价格大约为多少?
(Ⅱ) 电脑的价格大约每3年下降
| 2 |
| 3 |
考点:数列递推式,数列的应用
专题:等差数列与等比数列
分析:(Ⅰ)先由数列递推式求首项,然后结合an=Sn-Sn-1 求出n≥2时的通项公式,验证首项后得答案;
(Ⅱ)直接由题意列式求得9年后的价格.
(Ⅱ)直接由题意列式求得9年后的价格.
解答:
解:(Ⅰ)由Sn=-2n2+n-2,
当n=1时,a1=S1=-2×12+1-2=-3;
当n≥2时,an=Sn-Sn-1=-2n2+n-2-[-2(n-1)2+(n-1)-2]=3-4n.
验证n=1时上式不成立.
∴an=
;
(Ⅱ)∵电脑的价格大约每3年下降
,
∴三年后价格为之前的
,
则今年花8100元买的一台电脑,9年后的价格大约为8100×(1-
)3=300.
故9年后的价格大约为300元.
当n=1时,a1=S1=-2×12+1-2=-3;
当n≥2时,an=Sn-Sn-1=-2n2+n-2-[-2(n-1)2+(n-1)-2]=3-4n.
验证n=1时上式不成立.
∴an=
|
(Ⅱ)∵电脑的价格大约每3年下降
| 2 |
| 3 |
∴三年后价格为之前的
| 1 |
| 3 |
则今年花8100元买的一台电脑,9年后的价格大约为8100×(1-
| 2 |
| 3 |
故9年后的价格大约为300元.
点评:本题考查了数列的应用,考查了由数列的和求数列的通项公式,是中档题.

练习册系列答案
相关题目
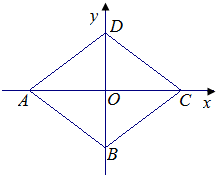 如图,在平面直角坐标系中,菱形ABCD的两个顶点C,D的坐标分别为(4,0),(0,3).现有两动点P,Q分别从A,C同时出发,点P沿线段AD以每秒1个单位的速度向终点D运动,点Q沿折线CBA以每秒2个单位的速度向终点A运动,设运动时间为t秒.
如图,在平面直角坐标系中,菱形ABCD的两个顶点C,D的坐标分别为(4,0),(0,3).现有两动点P,Q分别从A,C同时出发,点P沿线段AD以每秒1个单位的速度向终点D运动,点Q沿折线CBA以每秒2个单位的速度向终点A运动,设运动时间为t秒.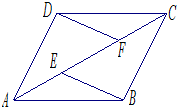 如图,E、F是四边形ABCD的对角线AC上的两点,AE=CF,BE=DF,BE∥DF,AD=DC求证:四边形ABCD是菱形.
如图,E、F是四边形ABCD的对角线AC上的两点,AE=CF,BE=DF,BE∥DF,AD=DC求证:四边形ABCD是菱形. 如图,是一个几何体的三视图,其中俯视图是正三角形,求:
如图,是一个几何体的三视图,其中俯视图是正三角形,求: 用红黄蓝三种颜色给如图所示的六连圆涂色,若每种颜色只能涂两个圆,且相邻两个圆所涂颜色不能相同,则不同的涂色方案共有
用红黄蓝三种颜色给如图所示的六连圆涂色,若每种颜色只能涂两个圆,且相邻两个圆所涂颜色不能相同,则不同的涂色方案共有