题目内容
设数列{an}的前n项和为Sn,点(n,
)(n∈N*)均在直线y=x+1上.
(1)求数列{an}的通项公式;
(2)设bn=3an,求数列{bn}的前n项和Tn.
| Sn |
| n |
(1)求数列{an}的通项公式;
(2)设bn=3an,求数列{bn}的前n项和Tn.
考点:数列的求和
专题:等差数列与等比数列
分析:(1)利用an与sn的关系求数列{an}的通项公式;
(2)由等比数列的求和公式求得结论.
(2)由等比数列的求和公式求得结论.
解答:
解:(1)∵点(n,
)(n∈N*)均在直线y=x+1上Sn=n2+n
当n≥2时,Sn-1=n2-n,an=Sn-Sn-1=2n;
当n=1时,a1=S1=2.
∴an=2n,n∈N*
(2)∵bn=3an=32n,
∴{bn}是首项为9,公比为9的等比数列.
∴Tn=b1+b2+b3+…+bn=9+92+93+…+9n=
(9n-1).
| Sn |
| n |
当n≥2时,Sn-1=n2-n,an=Sn-Sn-1=2n;
当n=1时,a1=S1=2.
∴an=2n,n∈N*
(2)∵bn=3an=32n,
∴{bn}是首项为9,公比为9的等比数列.
∴Tn=b1+b2+b3+…+bn=9+92+93+…+9n=
| 9 |
| 8 |
点评:本题主要考查利用数列与函数的关系及运用公式法求数列的通项公式等知识,考查学生运用等比数列的前n项和公式求数列的和的运算求解能力,属基础题.

练习册系列答案
 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案
相关题目
若某程序框图如图所示,当输入50时,则该程序运算后输出的结果是( )


| A、8 | B、6 | C、4 | D、2 |
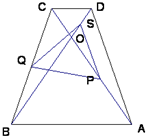 如图所示,等腰梯形ABCD中,AB∥CD,AD=CB,对角线AC与BD交于O,∠ACD=60°,点S、P、Q分别是OD、OA、BC的中点.
如图所示,等腰梯形ABCD中,AB∥CD,AD=CB,对角线AC与BD交于O,∠ACD=60°,点S、P、Q分别是OD、OA、BC的中点.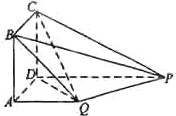 如图,四边形ABCD为正方形,PD⊥平面ABCD,PD∥QA,QA=AB=
如图,四边形ABCD为正方形,PD⊥平面ABCD,PD∥QA,QA=AB=