题目内容
(1)用分析法证明:
-
>
-
(2)已知a>0,b>0且a+b>2,求证:
,
中至少有一个小于2.
| 3 |
| 2 |
| 6 |
| 5 |
(2)已知a>0,b>0且a+b>2,求证:
| 1+b |
| a |
| 1+a |
| b |
考点:不等式的证明,反证法与放缩法
专题:证明题,分析法,反证法
分析:(Ⅰ)利用分析法,和两边平方法,即可证明结论;
(Ⅱ)利用了反证法,假设
,
都不小于2,则
≥2,
≥2,推得a+b≤2,这与已知a+b>2矛盾,故假设不成立,从而原结论成立.
(Ⅱ)利用了反证法,假设
| 1+b |
| a |
| 1+a |
| b |
| 1+b |
| a |
| 1+a |
| b |
解答:
证明:(1)要证:
-
>
-
,
即证:
+
>
+
,
即证:(
+
)2>(
+
)2,
即证:8+2
>8+2
,
即证:
>
,
即证:15>12.
而15>12显然成立,
所以:
-
>
-
---------------(6分)
(2)证明:假设
,
都不小于2,则
≥2,
≥2,
∵a>0,b>0,
∴1+b≥2a,1+a≥2b,
∴1+b+1+a≥2(a+b)
即a+b≤2,
这与已知a+b>2矛盾,故假设不成立,从而原结论成立.…(12分)
| 3 |
| 2 |
| 6 |
| 5 |
即证:
| 3 |
| 5 |
| 2 |
| 6 |
即证:(
| 3 |
| 5 |
| 2 |
| 6 |
即证:8+2
| 15 |
| 12 |
即证:
| 15 |
| 12 |
即证:15>12.
而15>12显然成立,
所以:
| 3 |
| 2 |
| 6 |
| 5 |
(2)证明:假设
| 1+b |
| a |
| 1+a |
| b |
| 1+b |
| a |
| 1+a |
| b |
∵a>0,b>0,
∴1+b≥2a,1+a≥2b,
∴1+b+1+a≥2(a+b)
即a+b≤2,
这与已知a+b>2矛盾,故假设不成立,从而原结论成立.…(12分)
点评:本题主要考查了推理论证的两种方法分析法和反证法,属于中档题.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案
相关题目
设a,b,c∈(0,+∞),则三个数a+
,b+
,c+
的值( )
| 1 |
| b |
| 1 |
| c |
| 1 |
| a |
| A、都大于2 |
| B、都小于2 |
| C、至少有一个不大于2 |
| D、至少有一个不小于2 |
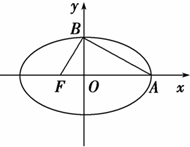 如图,椭圆的中心在坐标原点,F为左焦点,A,B分别为长轴和短轴上的一个顶点,当FB⊥AB时,此类椭圆称为“黄金椭圆”.类比“黄金椭圆”,可推出“黄金双曲线”的离心率为( )
如图,椭圆的中心在坐标原点,F为左焦点,A,B分别为长轴和短轴上的一个顶点,当FB⊥AB时,此类椭圆称为“黄金椭圆”.类比“黄金椭圆”,可推出“黄金双曲线”的离心率为( )A、
| ||||
B、
| ||||
C、
| ||||
D、
|
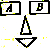 用黑、蓝2种颜色给如图所示的笑脸涂色,每个图形只能涂一种颜色,则两只眼睛(即图中A、B所示的区域)涂同种颜色而鼻子和嘴巴涂不同颜色的概率为( )
用黑、蓝2种颜色给如图所示的笑脸涂色,每个图形只能涂一种颜色,则两只眼睛(即图中A、B所示的区域)涂同种颜色而鼻子和嘴巴涂不同颜色的概率为( )