题目内容
已知函数f(x)=cos(
+x)cos(
-x)+
sinxcosx+
(Ⅰ)求函数f(x)的最小正周期和最大值;
(Ⅱ)若f(θ+
)=
,θ∈(
,
),求sin2θ的值.
| π |
| 3 |
| π |
| 3 |
| 3 |
| 1 |
| 4 |
(Ⅰ)求函数f(x)的最小正周期和最大值;
(Ⅱ)若f(θ+
| π |
| 12 |
| 1 |
| 3 |
| π |
| 4 |
| π |
| 2 |
考点:三角函数的周期性及其求法,二倍角的正弦
专题:三角函数的求值
分析:(Ⅰ)利用三角恒等变换可求得f(x)=sin(2x+
),从而可求得函数f(x)的最小正周期和最大值;
(Ⅱ)依题意知,sin(2θ+
)=
,利用同角三角函数间的关系式可求得cos(2θ+
)=-
,利用两角差的正弦即可求得sin2θ的值.
| π |
| 6 |
(Ⅱ)依题意知,sin(2θ+
| π |
| 3 |
| 1 |
| 3 |
| π |
| 3 |
2
| ||
| 3 |
解答:
解:(Ⅰ)f(x)=(cos
cosx-sin
sinx)(cos
cosx+sin
sinx)+
sin2x+
=
cos2x-
sin2x+
sin2x+
=
cos2x+
sin2x
=sin(2x+
),
∴函数f(x)的最小正周期T=
=π,最大值为1;
(Ⅱ)f(θ+
)=
,即sin(2θ+
)=
,
∵θ∈(
,
),2θ+
∈(
,
),
∴cos(2θ+
)=-
=-
,
∴sin2θ=sin(2θ+
-
)
=sin(2θ+
)cos
-cos(2θ+
)sin
=
×
-(-
)×
=
.
| π |
| 3 |
| π |
| 3 |
| π |
| 3 |
| π |
| 3 |
| ||
| 2 |
| 1 |
| 4 |
=
| 1 |
| 4 |
| 3 |
| 4 |
| ||
| 2 |
| 1 |
| 4 |
=
| 1 |
| 2 |
| ||
| 2 |
=sin(2x+
| π |
| 6 |
∴函数f(x)的最小正周期T=
| 2π |
| 2 |
(Ⅱ)f(θ+
| π |
| 12 |
| 1 |
| 3 |
| π |
| 3 |
| 1 |
| 3 |
∵θ∈(
| π |
| 4 |
| π |
| 2 |
| π |
| 3 |
| 5π |
| 6 |
| 4π |
| 3 |
∴cos(2θ+
| π |
| 3 |
1-(
|
2
| ||
| 3 |
∴sin2θ=sin(2θ+
| π |
| 3 |
| π |
| 3 |
=sin(2θ+
| π |
| 3 |
| π |
| 3 |
| π |
| 3 |
| π |
| 3 |
=
| 1 |
| 3 |
| 1 |
| 2 |
2
| ||
| 3 |
| ||
| 2 |
=
1+2
| ||
| 6 |
点评:本题考查三角恒等变换应用,着重考查三角函数的周期性、最值及其求法,考查同角三角函数间的关系式与两角差的正弦的综合应用,属于中档题.

练习册系列答案
相关题目
已知x,y满足约束条件
,则z=x+
y的最小值为( )
|
| 1 |
| 2 |
A、
| ||
B、
| ||
| C、1 | ||
| D、3 |
 已知抛物线C:y2=2px(p>0),M点的坐标为(12,8),N点在抛物线C上,且满足
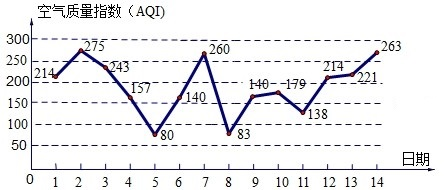
已知抛物线C:y2=2px(p>0),M点的坐标为(12,8),N点在抛物线C上,且满足 空气质量指数PM2.5(单位:μg/m3)表示每立方米空气中可入肺颗粒物的含量,这个值越高,就代表空气污染越严重:
空气质量指数PM2.5(单位:μg/m3)表示每立方米空气中可入肺颗粒物的含量,这个值越高,就代表空气污染越严重: