题目内容
2.已知函数f(x)=$\sqrt{3}$sinx•cosx-$\frac{1}{2}$cos2x(x∈R).(1)求函数f(x)的最小值和最小正周期;
(2)设△ABC的内角A,B,C的对边分别为a,b,c,且f(C)=1,B=30°,c=2$\sqrt{3}$,求△ABC的面积.
分析 (1)利用两角差的正弦函数公式化简解析式可得f(x)=sin(2x-$\frac{π}{6}$),结合正弦函数的性质及周期公式即可得解.
(2)由已知可得sin(2C-$\frac{π}{6}$)=1,可求范围-$\frac{π}{6}$<2C-$\frac{π}{6}$<$\frac{11π}{6}$,进而可求C,B,A,解得b的值,利用三角形面积公式即可计算得解.
解答 (本题满分为13分)
解:(1)∵f(x)=$\sqrt{3}$sinx•cosx-$\frac{1}{2}$cos2x=$\frac{\sqrt{3}}{2}$sin2x-$\frac{1}{2}$cos2x=sin(2x-$\frac{π}{6}$)…4分
∵x∈R,∴f(x)的最小值为-1…5分
∴最小正周期T=$\frac{2π}{2}$=π…6分
(2)∵f(C)=1,
∴sin(2C-$\frac{π}{6}$)=1,
∵0<2C<2π,可得:-$\frac{π}{6}$<2C-$\frac{π}{6}$<$\frac{11π}{6}$,
∴C=$\frac{π}{3}$…8分
∵B=$\frac{π}{6}$,可得:A=$\frac{π}{2}$,
∵c=2$\sqrt{3}$,可得:b=2,…12分
∴S△ABC=$\frac{1}{2}$bcsinA=2$\sqrt{3}$.…13分
点评 本题主要考查了两角差的正弦函数公式,正弦函数的图象和性质,周期公式,正弦定理,三角形面积公式在解三角形中的应用,考查了计算能力和转化思想,属于基础题.

练习册系列答案
 导学教程高中新课标系列答案
导学教程高中新课标系列答案
相关题目
13.把函数$y=sin(x+\frac{π}{4})$的图象向左平移$\frac{π}{4}$个单位长度,再将横坐标压缩到原来的$\frac{1}{2}$,所得函数的解析式为( )
| A. | y=sin2x | B. | $y=sin(2x+\frac{π}{8})$ | C. | y=cos2x | D. | $y=cos\frac{1}{2}x$ |
17.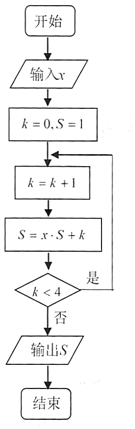 我国南宋数学家秦九韶(约公元1202-1261年)给出了求n(n∈N*)次多项式anxn+an-1xn-1+…+a1x+a0,当x=x0时的值的一种简捷算法.该算法被后人命名为“秦九韶算法”,例如,可将3次多项式改写为a3x3+a2x2+a1x+a0=((a3x+a2)x+a1)x+a0,然后进行求值.运行如图所示的程序框图,能求得多项式( )的值.
我国南宋数学家秦九韶(约公元1202-1261年)给出了求n(n∈N*)次多项式anxn+an-1xn-1+…+a1x+a0,当x=x0时的值的一种简捷算法.该算法被后人命名为“秦九韶算法”,例如,可将3次多项式改写为a3x3+a2x2+a1x+a0=((a3x+a2)x+a1)x+a0,然后进行求值.运行如图所示的程序框图,能求得多项式( )的值.
 我国南宋数学家秦九韶(约公元1202-1261年)给出了求n(n∈N*)次多项式anxn+an-1xn-1+…+a1x+a0,当x=x0时的值的一种简捷算法.该算法被后人命名为“秦九韶算法”,例如,可将3次多项式改写为a3x3+a2x2+a1x+a0=((a3x+a2)x+a1)x+a0,然后进行求值.运行如图所示的程序框图,能求得多项式( )的值.
我国南宋数学家秦九韶(约公元1202-1261年)给出了求n(n∈N*)次多项式anxn+an-1xn-1+…+a1x+a0,当x=x0时的值的一种简捷算法.该算法被后人命名为“秦九韶算法”,例如,可将3次多项式改写为a3x3+a2x2+a1x+a0=((a3x+a2)x+a1)x+a0,然后进行求值.运行如图所示的程序框图,能求得多项式( )的值.| A. | x4+x3+2x2+3x+4 | B. | x4+2x3+3x2+4x+5 | C. | x3+x2+2x+3 | D. | x3+2x2+3x+4 |
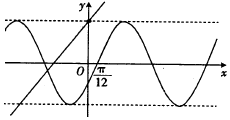 已知函数y=ksin(kx+φ)(|φ|<$\frac{π}{2}$)与函数y=kx-k2+6的部分图象如图所示,则φ=-$\frac{π}{6}$.
已知函数y=ksin(kx+φ)(|φ|<$\frac{π}{2}$)与函数y=kx-k2+6的部分图象如图所示,则φ=-$\frac{π}{6}$.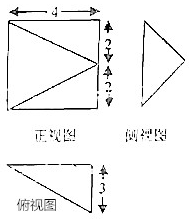 一个几何体的三视图如图所示,则该几何体的表面积是32+4$\sqrt{13}$.
一个几何体的三视图如图所示,则该几何体的表面积是32+4$\sqrt{13}$.