题目内容
10.某情报站有A,B,C,D四种互不相同的密码,每周使用其中的一种密码,且每周都是从上周未使用的三种密码中等可能地随机选用一种.设第1周使用A种密码,那么第7周也使用A种密码的概率是$\frac{61}{243}$.(用最简分数表示)分析 由题意可得,第n+1周也使用A种密码的概率 Pn+1=Pn•$\frac{1}{3}$,且P2=0,P3=$\frac{1}{3}$,以此类推可得第七周使用A的概率P7 的值.
解答 解:第一周使用A,第二周使用A的概率P2=0,第三周使用A的概率P3=$\frac{1}{3}$,依此类推,
第四周使用A的概率 P4=(1-$\frac{1}{3}$)•$\frac{1}{3}$=$\frac{2}{9}$,
第五周使用A的概率P5=(1-$\frac{2}{9}$)•$\frac{1}{3}$=$\frac{7}{27}$,
第六周使用A的概率P6=(1-P5)•$\frac{1}{3}$=$\frac{20}{81}$,
第七周使用A的概率P7=(1-P6)•$\frac{1}{3}$=$\frac{61}{243}$.
故答案为$\frac{61}{243}$.
点评 此题主要考查了概率公式,得到第n+1周也使用A种密码的概率 Pn+1=Pn•$\frac{1}{3}$是解题的关键,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
20.运行如图所示的程序框图,则输出的a的值为( )
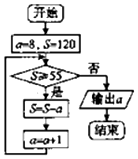

| A. | 13 | B. | 14 | C. | 15 | D. | 16 |
5.定义运算a*b为执行如图所示的程序框图输出的S值,则${100^{(\frac{1}{2}lg9-lg2)}}*({log_9}8•{log_4}\root{3}{3})$的值为( )
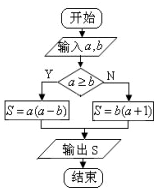

| A. | $\frac{13}{16}$ | B. | $\frac{9}{2}$ | C. | 4 | D. | 6 |
18.若圆C:x2+y2=4上的点到直线l:y=x+a的最小距离为2,则a=( )
| A. | $2\sqrt{2}$ | B. | $4\sqrt{2}$ | C. | $±2\sqrt{2}$ | D. | $±4\sqrt{2}$ |



