题目内容
9．
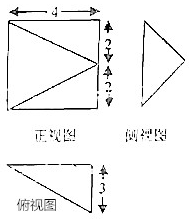一个几何体的三视图如图所示，则该几何体的表面积是32+4$\sqrt{13}$．
分析 根据几何体的直观图知该几何体是一四棱锥，
画出图形，结合图中数据求出它的表面积．
解答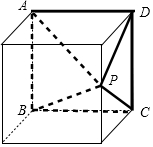 
解：根据几何体的直观图知，它是一四棱锥，如图中粗线所示；
结合图中数据，计算它的表面积为
S=S正方形ABCD+S△PCD+2S△PAD+S△PAB
=42+$\frac{1}{2}$×4×3+2×$\frac{1}{2}$×4×$\sqrt{{3}^{2}{+2}^{2}}$+$\frac{1}{2}$×4×$\sqrt{{4}^{2}{+3}^{2}}$=32+4$\sqrt{13}$．
故答案为：32+4$\sqrt{13}$．
点评 本题考查了根据几何体三视图求表面积的应用问题，是基础题．
练习册系列答案
相关题目
1．椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1（a＞b＞0）$，F1，F2为椭圆的左、右焦点，O为坐标原点，点P为椭圆上一点，$|OP|=\frac{{\sqrt{2}}}{4}a$，且|PF1|，|F1F2|，|PF2|成等比数列，则椭圆的离心率为（ ）
| A． | $\frac{{\sqrt{2}}}{4}$ | B． | $\frac{{\sqrt{2}}}{3}$ | C． | $\frac{{\sqrt{6}}}{3}$ | D． | $\frac{{\sqrt{6}}}{4}$ |
18．若圆C：x2+y2=4上的点到直线l：y=x+a的最小距离为2，则a=（ ）
| A． | $2\sqrt{2}$ | B． | $4\sqrt{2}$ | C． | $±2\sqrt{2}$ | D． | $±4\sqrt{2}$ |
19．已知某几何体的三视图如图所示，则该几何体的体积为（ ）
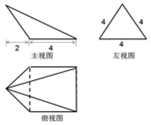
| A． | $\frac{32}{3}$ | B． | $\frac{{16\sqrt{3}}}{3}$ | C． | $\frac{{32\sqrt{3}}}{3}$ | D． | $\frac{{64\sqrt{3}}}{3}$ |