题目内容
5.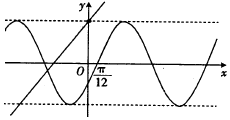 已知函数y=ksin(kx+φ)(|φ|<$\frac{π}{2}$)与函数y=kx-k2+6的部分图象如图所示,则φ=-$\frac{π}{6}$.
已知函数y=ksin(kx+φ)(|φ|<$\frac{π}{2}$)与函数y=kx-k2+6的部分图象如图所示,则φ=-$\frac{π}{6}$.
分析 根据直线过点(0,|k|)和单调性计算k,把($\frac{π}{12}$,0)代入y=ksin(kx+φ)即可求出φ.
解答 解:函数y=ksin(kx+φ)的最大值为|k|,
∵函数y=kx-k2+6是增函数,且经过点(0,|k|),
∴$\left\{\begin{array}{l}{k>0}\\{-{k}^{2}+6=k}\end{array}\right.$,
解得k=2,
∴三角函数解析式为y=2sin(2x+φ),
∵此函数经过点($\frac{π}{12}$,0),
∴2sin($\frac{π}{6}$+φ)=0,即$\frac{π}{6}$+φ=kπ,解得φ=-$\frac{π}{6}$+kπ,k∈Z.
∵|φ|<$\frac{π}{2}$,∴φ=-$\frac{π}{6}$.
故答案为:$-\frac{π}{6}$.
点评 本题考查了三角函数的图象与性质,属于基础题.

练习册系列答案
 教学练新同步练习系列答案
教学练新同步练习系列答案 课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案
相关题目
17.设函数$f(x)=cos(2x-\frac{π}{2})$,x∈R,则f(x)是( )
| A. | 最小正周期为π的奇函数 | B. | 最小正周期为π的偶函数 | ||
| C. | 最小正周期为$\frac{π}{2}$的奇函数 | D. | 最小正周期为$\frac{π}{2}$的偶函数 |




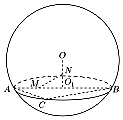 如图,用一平面去截球O,所得截面面积为16π,球心O到截面的距离为3,O1为截面小圆圆心,AB为截面小圆的直径;
如图,用一平面去截球O,所得截面面积为16π,球心O到截面的距离为3,O1为截面小圆圆心,AB为截面小圆的直径;