题目内容
13.把函数$y=sin(x+\frac{π}{4})$的图象向左平移$\frac{π}{4}$个单位长度,再将横坐标压缩到原来的$\frac{1}{2}$,所得函数的解析式为( )| A. | y=sin2x | B. | $y=sin(2x+\frac{π}{8})$ | C. | y=cos2x | D. | $y=cos\frac{1}{2}x$ |
分析 利用诱导公式,y=Asin(ωx+φ)的图象变换规律,得出结论.
解答 解:把函数$y=sin(x+\frac{π}{4})$的图象向左平移$\frac{π}{4}$个单位长度,可得y=sin(x+$\frac{π}{2}$)=cosx的图象;
再将横坐标压缩到原来的$\frac{1}{2}$,所得函数的解析式为y=cos2x,
故选:C.
点评 本题主要考查诱导公式,y=Asin(ωx+φ)的图象变换规律,属于基础题.

练习册系列答案
相关题目
5.定义运算a*b为执行如图所示的程序框图输出的S值,则${100^{(\frac{1}{2}lg9-lg2)}}*({log_9}8•{log_4}\root{3}{3})$的值为( )
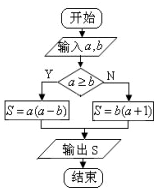

| A. | $\frac{13}{16}$ | B. | $\frac{9}{2}$ | C. | 4 | D. | 6 |
1.椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$,F1,F2为椭圆的左、右焦点,O为坐标原点,点P为椭圆上一点,$|OP|=\frac{{\sqrt{2}}}{4}a$,且|PF1|,|F1F2|,|PF2|成等比数列,则椭圆的离心率为( )
| A. | $\frac{{\sqrt{2}}}{4}$ | B. | $\frac{{\sqrt{2}}}{3}$ | C. | $\frac{{\sqrt{6}}}{3}$ | D. | $\frac{{\sqrt{6}}}{4}$ |