题目内容
12.已知边长为2$\sqrt{3}$的菱形ABCD中,∠BAD=60°,沿对角边BD折成二面角A-BD-C为120°的四面体ABCD,则四面体的外接球的表面积为28π.分析 设两三角形外心分别为O2,O3,球心为O,BD中点为O1,由题意知∠AO1C=120°,OO1=2,OO3=$\sqrt{3}$,由此求出球半径,从而能求出四面体的外接球的表面积.
解答 解:如图,设两三角形外心分别为O2,O3,球心为O,BD中点为O1,
由题意知∠AO1C=120°,
∴OO1=2,OO3=$\sqrt{3}$,
∴球半径OC=$\sqrt{{2}^{2}+(\sqrt{3})^{2}}$=$\sqrt{7}$,
∴四面体的外接球的表面积为S=4$π×(\sqrt{7})^{2}$=28π.
故答案为:28π.
点评 本题主要考查了四面体外接球的表面积的求法,考查推理论证能力、运算求解能力、空间思维能力,考查转化化归思想、数形结合思想,是中档题.

练习册系列答案
相关题目
5.定义运算a*b为执行如图所示的程序框图输出的S值,则${100^{(\frac{1}{2}lg9-lg2)}}*({log_9}8•{log_4}\root{3}{3})$的值为( )
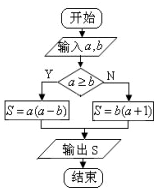

| A. | $\frac{13}{16}$ | B. | $\frac{9}{2}$ | C. | 4 | D. | 6 |
1.椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$,F1,F2为椭圆的左、右焦点,O为坐标原点,点P为椭圆上一点,$|OP|=\frac{{\sqrt{2}}}{4}a$,且|PF1|,|F1F2|,|PF2|成等比数列,则椭圆的离心率为( )
| A. | $\frac{{\sqrt{2}}}{4}$ | B. | $\frac{{\sqrt{2}}}{3}$ | C. | $\frac{{\sqrt{6}}}{3}$ | D. | $\frac{{\sqrt{6}}}{4}$ |
2.如图画的某几何体的三视图,网格纸上小正方形的边长为1,则该几何体的表面积为( )

| A. | $144+2\sqrt{10}π$ | B. | $144+({2\sqrt{10}-2})π$ | C. | $128+2\sqrt{10}π$ | D. | $128+({2\sqrt{10}-2})π$ |



