题目内容
3.数列{an}的前n项和为Sn,若Sn=2an-1,则an=2n-1.分析 根据已知等式确定出Sn-1=2an-1-1(n>1),已知等式与所得等式相减,利用数列的递推式得到数列{an}为首项是1,公比是2的等比数列,利用等比数列性质确定出通项公式即可.
解答 解:∵Sn=2an-1①,
∴Sn-1=2an-1-1②(n>1),
①-②得:Sn-Sn-1=2an-2an-1,即an=2an-2an-1,
整理得:an=2an-1,即$\frac{{a}_{n}}{{a}_{n-1}}$=2,
∵S1=a1=2a1-1,即a1=1,
∴数列{an}为首项是1,公比是2的等比数列,
则an=2n-1.
故答案为:2n-1
点评 此题考查了数列的递推式,等比数列的性质,解题的关键是由递推公式推导数列的通项公式.

练习册系列答案
相关题目
13.抛物线y=$\frac{{x}^{2}}{4}$的焦点为F,点P在抛物线上,若|PF|=5,则点P到y轴的距离为( )
| A. | 6 | B. | 5$\sqrt{2}$ | C. | 5 | D. | 4 |
11.对于数25,规定第1次操作为23+53=133,第2次操作为13+33+33=55,如此反复操作,则第2016次操作后得到的数是( )
| A. | 25 | B. | 250 | C. | 55 | D. | 133 |
15.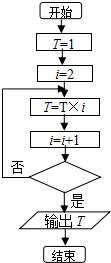 若如图程序框图的输出结果为120,则判断框中应填写的判断条件为( )
若如图程序框图的输出结果为120,则判断框中应填写的判断条件为( )
 若如图程序框图的输出结果为120,则判断框中应填写的判断条件为( )
若如图程序框图的输出结果为120,则判断框中应填写的判断条件为( )| A. | i<5? | B. | i>5? | C. | i>6? | D. | i≥5? |
12.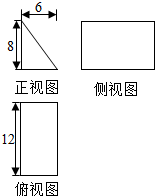 一块石材表示的几何体的三视图如图所示,将该石材切削、打磨,加工成球,则能得到的最大球的表面积等于( )
一块石材表示的几何体的三视图如图所示,将该石材切削、打磨,加工成球,则能得到的最大球的表面积等于( )
 一块石材表示的几何体的三视图如图所示,将该石材切削、打磨,加工成球,则能得到的最大球的表面积等于( )
一块石材表示的几何体的三视图如图所示,将该石材切削、打磨,加工成球,则能得到的最大球的表面积等于( )| A. | $\frac{32π}{3}$ | B. | 16π | C. | 32π | D. | $\frac{16π}{3}$ |
13.已知椭圆:$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1$(a>b>0),F1,F2为椭圆的左右焦点,M是椭圆上任一点,若$\overrightarrow{M{F}_{1}}$•$\overrightarrow{M{F}_{2}}$的取值范围是[-4,4],则椭圆的方程为( )
| A. | $\frac{{x}^{2}}{8}$+$\frac{{y}^{2}}{4}$=1 | B. | $\frac{{x}^{2}}{12}$+$\frac{{y}^{2}}{8}$=1 | C. | $\frac{{x}^{2}}{12}$+$\frac{{y}^{2}}{4}$=1 | D. | $\frac{{x}^{2}}{4}$+y2=1 |

