题目内容
12．
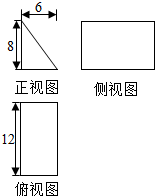一块石材表示的几何体的三视图如图所示，将该石材切削、打磨，加工成球，则能得到的最大球的表面积等于（ ）| A． | $\frac{32π}{3}$ | B． | 16π | C． | 32π | D． | $\frac{16π}{3}$ |
分析 几何体为三棱柱，若内切球面积最大，则球的大圆为棱柱底面三角形的内切圆．
解答 解：由三视图可知几何体为底面是直角三角形的直三棱柱．若要使其内切球最大，则球的大圆为底面三角形的内切圆．
由三视图可知棱柱的底面为主视图中的三角形，直角边分别为6，8，斜边为10．
设最大球半径为r，则6-r+8-r=10，解得r=2．
∴最大球的表面积为4πr2=16π．
故选B．
点评 本题考查了多面体与内切球的相关知识，寻找球与多面体的关系是关键．
练习册系列答案
全优考典单元检测卷及归类总复习系列答案
相关题目
2．
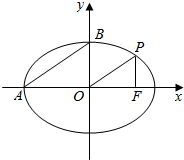如图所示，点P在椭圆$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1$（a＞b＞0）上，F（c，0）是椭圆的右焦点，点A、B是椭圆的顶点，若PF⊥x轴，且$\frac{|OP|}{|AB|}$=$\frac{c}{a}$，则椭圆的离心率是（ ）
如图所示，点P在椭圆$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1$（a＞b＞0）上，F（c，0）是椭圆的右焦点，点A、B是椭圆的顶点，若PF⊥x轴，且$\frac{|OP|}{|AB|}$=$\frac{c}{a}$，则椭圆的离心率是（ ）| A． | $\frac{1}{2}$ | B． | $\frac{\sqrt{2}}{2}$ | C． | $\frac{1}{3}$ | D． | $\frac{\sqrt{3}}{3}$ |