题目内容
14．某个几何体的三视图如图所示，则该几何体的体积是1
分析 几何体为三棱锥，底面为直角三角形，高为1．
解答 解：由三视图可知几何体为三棱锥，底面为俯视图中的直角三角形，棱锥的高为1．
∴三棱锥的体积V=$\frac{1}{3}×\frac{1}{2}×2×3×1$=1．
故答案为1．
点评 本题考查了棱锥的三视图和结构特征，体积计算，属于基础题．
练习册系列答案
阅读快车系列答案
相关题目
2．
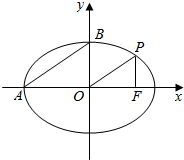如图所示，点P在椭圆$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1$（a＞b＞0）上，F（c，0）是椭圆的右焦点，点A、B是椭圆的顶点，若PF⊥x轴，且$\frac{|OP|}{|AB|}$=$\frac{c}{a}$，则椭圆的离心率是（ ）
如图所示，点P在椭圆$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1$（a＞b＞0）上，F（c，0）是椭圆的右焦点，点A、B是椭圆的顶点，若PF⊥x轴，且$\frac{|OP|}{|AB|}$=$\frac{c}{a}$，则椭圆的离心率是（ ）| A． | $\frac{1}{2}$ | B． | $\frac{\sqrt{2}}{2}$ | C． | $\frac{1}{3}$ | D． | $\frac{\sqrt{3}}{3}$ |
9．“?x∈R，x2-2＞0”的否定是（ ）
| A． | ?x∈R，x2-2＜0 | B． | ?x∈R，x2-2≤0 | ||
| C． | ?x0∈R，x${\;}_{0}^{2}$-2＜0 | D． | ?x0∈R，x${\;}_{0}^{2}$-2≤0 |