题目内容
在平面直角坐标xOy中,设圆M的半径为1,圆心在直线x-y-1=0上,若圆M上不存在点N,使NO=
NA,其中A(0,3),则圆心M横坐标的取值范围 .
| 1 |
| 2 |
考点:轨迹方程,圆的标准方程
专题:圆锥曲线的定义、性质与方程
分析:求出N的轨迹方程,然后判断所求轨迹方程与圆的方程没有解即可.
解答:
解:设N(x,y),NO=
NA,其中A(0,3),
∴
=
,
解得N的轨迹方程为:x2+(y+1)2=4,y圆心坐标Q(0,-1),半径为2,
在平面直角坐标xOy中,设圆M的半径为1,圆心在直线x-y-1=0上,若圆M上不存在点N,使NO=
NA,
则M所在位置如图:M的横坐标在C、F两点的外侧,D、E两点之间,
圆心M横坐标的取值范围:(-∞,-
)∪(-
,
)∪(
,+∞)
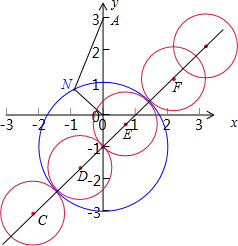
(-∞,0)∪(
,+∞).
故答案为:(-∞,-
)∪(-
,
)∪
(
,+∞).
| 1 |
| 2 |
∴
| x2+y2 |
| 1 |
| 2 |
| x2+(y-3)2 |
解得N的轨迹方程为:x2+(y+1)2=4,y圆心坐标Q(0,-1),半径为2,
在平面直角坐标xOy中,设圆M的半径为1,圆心在直线x-y-1=0上,若圆M上不存在点N,使NO=
| 1 |
| 2 |
则M所在位置如图:M的横坐标在C、F两点的外侧,D、E两点之间,
圆心M横坐标的取值范围:(-∞,-
3
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
3
| ||
| 2 |
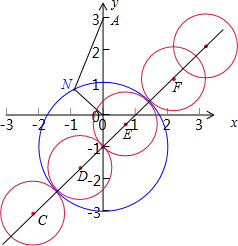
(-∞,0)∪(
| 12 |
| 5 |
故答案为:(-∞,-
3
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
(
3
| ||
| 2 |
点评:本题考查圆的方程的综合应用,轨迹方程的求法,考查数形结合思想的应用.

练习册系列答案
相关题目
设双曲线
-
=1(a>0)的渐近线方程为3x±2y=0,则a的值为( )
| x2 |
| a2 |
| y2 |
| 9 |
| A、4 | B、3 | C、2 | D、1 |
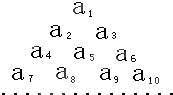 已知数列{an}是首项为1,公差为2的等差数列,将数列{an}中的各项排成如图所示的一个三角形数表,记A(i,j)表示第i行从左至右的第j个数,例如A(4,3)=a9,则A(10,4)=
已知数列{an}是首项为1,公差为2的等差数列,将数列{an}中的各项排成如图所示的一个三角形数表,记A(i,j)表示第i行从左至右的第j个数,例如A(4,3)=a9,则A(10,4)=