题目内容
已知函数f(x)=sin2x-
cos2x+1,x∈[
,
].
(1)求f(x)的最大值和最小值;
(2)若不等式|f(x)-m|<2在x∈[
,
]上恒成立,求实数m的取值范围.
(3)将函数y=f(x)的图象向右平移
个单位,得到y=g(x)的图象,求直线y=2+
与函数y=f(x)+g(x)的图象在(-π,π)内所有交点的坐标.
| 3 |
| π |
| 4 |
| π |
| 2 |
(1)求f(x)的最大值和最小值;
(2)若不等式|f(x)-m|<2在x∈[
| π |
| 4 |
| π |
| 2 |
(3)将函数y=f(x)的图象向右平移
| π |
| 4 |
| 2 |
考点:三角函数的最值,函数y=Asin(ωx+φ)的图象变换
专题:三角函数的求值
分析:(1)根据函数f(x)=2sin(2x-
)+1,x∈[
,
],利用正弦函数的定义域和值域,求得f(x)的最大值和最小值.
(2)由条件可得
<sin(2x-
)<
在x∈[
,
]上恒成立,结合f(x)的值域可得
<
,且
>1,由此求得实数m的取值范围.
(3)由条件根据函数y=Asin(ωx+φ)的图象变换规律可得y=g(x)=-2cos(2x-
)+1,再根据x∈(-π,π),可得 2x-
∈(-2π-
,2π-
).由y=2+
=f(x)+g(x),求得cos(2x-
)=-1,求得x的值,可得直线y=2+
与函数y=f(x)+g(x)的图象在(-π,π)内所有交点的坐标.
| π |
| 3 |
| π |
| 4 |
| π |
| 2 |
(2)由条件可得
| m-3 |
| 2 |
| π |
| 3 |
| m+1 |
| 2 |
| π |
| 4 |
| π |
| 2 |
| m-3 |
| 2 |
| 1 |
| 2 |
| m+1 |
| 2 |
(3)由条件根据函数y=Asin(ωx+φ)的图象变换规律可得y=g(x)=-2cos(2x-
| π |
| 3 |
| π |
| 12 |
| π |
| 12 |
| π |
| 12 |
| 2 |
| π |
| 12 |
| 2 |
解答:
解:(1)∵函数f(x)=sin2x-
cos2x+1=2sin(2x-
)+1,
∵x∈[
,
].∴2x-
∈[
,
],sin(2x-
)∈[
,1],
∴当2x-
=
时,函数取得最小值为2,当2x-
=
时,函数取得最大值为3.
(2)若不等式|f(x)-m|<2在x∈[
,
]上恒成立,即
<sin(2x-
)<
在x∈[
,
]上恒成立,
∴
<
,且
>1,由此求得m>1,或 m<4,由此求得实数m的取值范围为{m|m>1,或 m<4}.
(3)将函数y=f(x)的图象向右平移
个单位,得到y=g(x)=2sin[2(x-
)-
]+1=2sin(2x-
-
)+1=-2cos(2x-
)+1 的图象,
故y=f(x)+g(x)=2sin(2x-
)+1+-2cos(2x-
)+1=2+2
sin(2x-
-
)=2+2
sin(2x-
)=2-2
cos(2x-
).
再根据x∈(-π,π),可得 2x-
∈(-2π-
,2π-
).
由y=2+
=f(x)+g(x),求得cos(2x-
)=-1,求得2x-
=-π 或2x-
=π,即x=-
,或x=
.
故直线y=2+
与函数y=f(x)+g(x)的图象在(-π,π)内所有交点的坐标分别为(-
,2+
),(
,2+
).
| 3 |
| π |
| 3 |
∵x∈[
| π |
| 4 |
| π |
| 2 |
| π |
| 3 |
| π |
| 6 |
| 2π |
| 3 |
| π |
| 3 |
| 1 |
| 2 |
∴当2x-
| π |
| 3 |
| π |
| 6 |
| π |
| 3 |
| π |
| 2 |
(2)若不等式|f(x)-m|<2在x∈[
| π |
| 4 |
| π |
| 2 |
| m-3 |
| 2 |
| π |
| 3 |
| m+1 |
| 2 |
| π |
| 4 |
| π |
| 2 |
∴
| m-3 |
| 2 |
| 1 |
| 2 |
| m+1 |
| 2 |
(3)将函数y=f(x)的图象向右平移
| π |
| 4 |
| π |
| 4 |
| π |
| 3 |
| π |
| 2 |
| π |
| 3 |
| π |
| 3 |
故y=f(x)+g(x)=2sin(2x-
| π |
| 3 |
| π |
| 3 |
| 2 |
| π |
| 3 |
| π |
| 4 |
| 2 |
| 7π |
| 12 |
| 2 |
| π |
| 12 |
再根据x∈(-π,π),可得 2x-
| π |
| 12 |
| π |
| 12 |
| π |
| 12 |
由y=2+
| 2 |
| π |
| 12 |
| π |
| 12 |
| π |
| 12 |
| 11π |
| 24 |
| 13π |
| 24 |
故直线y=2+
| 2 |
| 11π |
| 24 |
| 2 |
| 13π |
| 24 |
| 2 |
点评:本题主要考查利用诱导公式进行化简求值,正弦函数的定义域和值域,函数的恒成立问题,函数y=Asin(ωx+φ)的图象变换规律,体现了转化的数学思想,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
下列函数中周期为π且图象关于直线x=
对称的函数是( )
| π |
| 6 |
A、y=2sin(2x-
| ||||
B、y=2sin(
| ||||
C、y=2sin(2x+
| ||||
D、y=2sin(
|
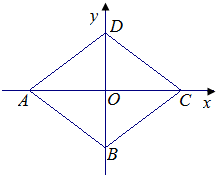 如图,在平面直角坐标系中,菱形ABCD的两个顶点C,D的坐标分别为(4,0),(0,3).现有两动点P,Q分别从A,C同时出发,点P沿线段AD以每秒1个单位的速度向终点D运动,点Q沿折线CBA以每秒2个单位的速度向终点A运动,设运动时间为t秒.
如图,在平面直角坐标系中,菱形ABCD的两个顶点C,D的坐标分别为(4,0),(0,3).现有两动点P,Q分别从A,C同时出发,点P沿线段AD以每秒1个单位的速度向终点D运动,点Q沿折线CBA以每秒2个单位的速度向终点A运动,设运动时间为t秒. 如图,是一个几何体的三视图,其中俯视图是正三角形,求:
如图,是一个几何体的三视图,其中俯视图是正三角形,求: