题目内容

已知f（x）=（x+1）（x-1）（x+2），求f′（x），f′（2），[f（2）]′．
考点：导数的运算
专题：导数的概念及应用
分析：根据导数的运算法则求导即可，然后再代入值求得结果．
解答： 解：∵f（x）=（x+1）（x-1）（x+2）=x3+2x2-x-2，
∴f′（x）=3x2+4x-1，
∴f′（2）=3×4+4×2-1=19，
∵f（2）为常数，
∴[f（2）]′=0．
点评：本题主要考查了导数的运算法则，注意f（2）为常数，常数的导数为0，属于基础题．
练习册系列答案
相关题目
下列命题中，真命题是（　　）
A、空间不同三点确定一个平面
B、空间两两相交的三条直线确定一个平面
C、两组对边相等的四边形是平行四边形
D、和同一直线都相交的三条平行线在同一平面内
用分析法证明：
a
-
a-1
＜
a-2
-
a-3
（a≥3）．
设函数f（x）=x3-3mx+n（m＞0）的极大值为6，极小值为2，求：
（Ⅰ）实数m，n的值；            
（Ⅱ）f（x）在区间[0，3]上的最大值和最小值．
已知关于x的二次函数y=ax2+bx+c（a＞0）的图象经过点C（0，2），且与x轴交于不同的两点A、B，点A的坐标是（1，0）．
（1）求a的取值范围；
（2）该二次函数的图象与直线y=2交于C、D两点，设A、B、C、D四点构成的四边形的对角线相交于点P，记△PCD的面积为S1，△PAB的面积为S2，当a＞2时，试探索S1-S2是否为常数，若是求出该常数，若不是请说明理由．（提示：请先根据题目条件在给定的平面直角坐标系中画出示意图）
已知函数f（x）=sin2x-
3
cos2x+1，x∈[
π
4
，
π
2
]．
（1）求f（x）的最大值和最小值；
（2）若不等式|f（x）-m|＜2在x∈[
π
4
，
π
2
]上恒成立，求实数m的取值范围．
（3）将函数y=f（x）的图象向右平移
π
4
个单位，得到y=g（x）的图象，求直线y=2+
2
与函数y=f（x）+g（x）的图象在（-π，π）内所有交点的坐标．
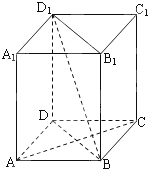如图，在四棱柱ABCD-A1B1C1D1中，D1D⊥底面ABCD，底面ABCD是正方形，且AB=1，D1D=
2
．
（1）求直线D1B与平面ABCD所成角的大小；
（2）求证：AC⊥平面BB1D1D．
已知数列{an}满足a1=5，a2=5，an+1=an+6an-1，（n≥2，n∈N*）．
（Ⅰ）求证数列{an+1+2an}是等比数列；
（Ⅱ）求出所有使数列{an+1+λan}成等比数列的λ的值；
（Ⅲ）求数列{an}的通项公式．
已知函数f（x）=x+alnx（a∈R）．
（I）若a=-1时，求曲线y=f（x）在点x=1处的切线方程；
（Ⅱ）若a≤0，函数f（x）没有零点，求a的取值范围．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网