题目内容
解不等式:
-
<
.
| 1 | ||
|
| 1 | ||
|
| 2 | ||
|
考点:组合及组合数公式
专题:排列组合
分析:利用组合数公式把不等式化简,求出解集即可.
解答:
解:∵不等式为
-
<
,
∴
-
<
(n>4,且n∈N*),
即1-
<
,
化简得2n2-9n-11>0;
解得n<-1,或n>
,
∴原不等式的解集为{n|n≥6,且n∈N*}.
| 1 | ||
|
| 1 | ||
|
| 2 | ||
|
∴
| n(n-1)(n-2) |
| 3! |
| n(n-1)(n-2)(n-3) |
| 4! |
| 2n(n-1)(n-2)(n-3)(n-4) |
| 5! |
即1-
| n-3 |
| 4 |
| (n-3)(n-4) |
| 2×5 |
化简得2n2-9n-11>0;
解得n<-1,或n>
| 11 |
| 2 |
∴原不等式的解集为{n|n≥6,且n∈N*}.
点评:本题考查了组合数公式的应用问题,也考查了一元二次不等式的解法与应用问题,是基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
函数f(x)=sin(2ωx-
)(ω>0)图象的一个对称中心到最近对称轴的距离为
,则ω的值为( )
| π |
| 3 |
| π |
| 4 |
A、
| ||
B、
| ||
| C、1 | ||
| D、2 |
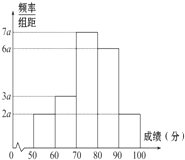 从100名学生中抽取20名学生某次数学考试成绩(单位:分)的频率分布直方图如下:
从100名学生中抽取20名学生某次数学考试成绩(单位:分)的频率分布直方图如下: