Question

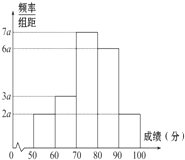从100名学生中抽取20名学生某次数学考试成绩（单位：分）的频率分布直方图如下：
（1）求频率分布直方图中a的值；
（2）估计总体中成绩落在[50，70）中的学生人数；
（3）估计总体的中位数．

Answer 1

考点：频率分布直方图

专题：概率与统计

分析：（1）根据频率分布直方图中各频率和等于1，求出a的值；
（2）求出成绩在[50，70）中的频率，即可求出对应的频数；
（3）利用中位数两边的频率相等，求出总体的中位数值．

解答： 解：（1）根据频率分布直方图，得；
（2a+3a+7a+6a+2a）×10=1，
解得a=

1

200

；
（2）成绩在[50，70）中的频率是
2×

1

200

×10+3×

1

200

×10=

1

4

，
∴成绩在[50，70）中的学生数是
100×

1

4

=25；
（3）∵2×

1

200

×10+3×

1

200

×10=

1

4

＜

1

2

，

1

4

+7×

1

200

×10=

3

5

＞

1

2

，
∴令

1

4

+7×

1

200

•x=

1

2

，
解得x=

50

7

；
∴估计总体的中位数为70+

50

7

=

540

7

．

点评：本题考查了频率分布直方图的应用问题，也考查了求数据的数字特征的应用问题，是基础题．