题目内容
已知a2+b2=x2,c2+d2=y2,a,d,c,b,x,y∈R+,求证xy≥ac+bd.
考点:不等式的证明
专题:证明题
分析:首先由等式a2+b2=x2,c2+d2=y2求证xy≥ac+bd.把已知条件代入得到x2y2=(a2+b2)(c2+d2),展开再根据基本不等式证明求解,即可得到结果.
解答:
解:已知a2+b2=x2,c2+d2=y2
所以x2y2=(a2+b2)(c2+d2)=a2c2+b2c2+b2d2+a2d2≥a2c2+2abcd+b2d2=(ac+bd)2
又因x,y,a,b,c,d都是正数,上式两边开方得xy≥ac+bd.
故得证.
所以x2y2=(a2+b2)(c2+d2)=a2c2+b2c2+b2d2+a2d2≥a2c2+2abcd+b2d2=(ac+bd)2
又因x,y,a,b,c,d都是正数,上式两边开方得xy≥ac+bd.
故得证.
点评:此题主要考查基本不等式的证明问题,有一定的技巧性,在做题的时候同学们要注意认真分析,才能选择出较容易的方法解题.

练习册系列答案
 快捷英语周周练系列答案
快捷英语周周练系列答案
相关题目
直线l与平面a内的两条直线都垂直,则直线l与平面a的位置关系是( )
| A、平行 | B、垂直 |
| C、在平面a内 | D、无法确定 |
a≥0,b≥0,a+b=1,且x1,x2为正数,y1=ax1+bx2,y2=bx1+ax2,则y1y2与x1x2的大小关系是( )
| A、y1y2≥x1x2 |
| B、y1y2≤x1x2 |
| C、y1y2>x1x2 |
| D、y1y2<x1x2 |
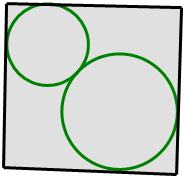 如图,在单位正方形内作两个互相外切的圆,同时每一个圆又与正方形的两相邻边相切,记其中一个圆的半径为x,两圆的面积之和为S,将S表示为x的函数,求函数S=f(x)的解析式及f(x)的值域.
如图,在单位正方形内作两个互相外切的圆,同时每一个圆又与正方形的两相邻边相切,记其中一个圆的半径为x,两圆的面积之和为S,将S表示为x的函数,求函数S=f(x)的解析式及f(x)的值域. 、
、 满足
满足 ,则
,则 的最小值为( )
的最小值为( ) (C)
(C) (D)
(D)
 的公差
的公差 ,且
,且 成等比数列,若
成等比数列,若 是数列
是数列 项的和,则
项的和,则 的最小值为( )
的最小值为( ) D.
D.