题目内容
已知y=f(x)是偶函数,且在[0,+∞)上是减函数,则f(1-x2)是增函数的区间是( )
| A、[0,+∞) |
| B、(-∞,0] |
| C、[-1,0)∪(1,+∞) |
| D、(-∞,-1]∪(0,1] |
考点:奇偶性与单调性的综合
专题:计算题
分析:y=f(x)是偶函数,且在[0,+∞)上是减函数,∴在(-∞,0]是增函数,
复合函数的单调性:y=f(t),t=u(x),当f(t)与u(x)都是增函数,或都是减函数时,
y=f(u(x))才是增函数.
复合函数的单调性:y=f(t),t=u(x),当f(t)与u(x)都是增函数,或都是减函数时,
y=f(u(x))才是增函数.
解答:
解:∵y=f(x)是偶函数,且在[0,+∞)上是减函数,
∴在(-∞,0]是增函数,
令t=1-x2 ,要使f(t)是增函数,应有t≤0 时t是增函数,或者t≥0时,t是减函数.
∵t≤0时,有 x≥1 或x≤-1,
t=1-x2 在(-∞,-1]上是增函数,f(1-x2)是增函数,
t≥0时,1≥x≥-1,
t=1-x2 在(0,1]上是减函数,f(1-x2)是增函数,
则f(1-x2)是增函数的区间是 (-∞,-1]∪(0,1],
故选 D.
∴在(-∞,0]是增函数,
令t=1-x2 ,要使f(t)是增函数,应有t≤0 时t是增函数,或者t≥0时,t是减函数.
∵t≤0时,有 x≥1 或x≤-1,
t=1-x2 在(-∞,-1]上是增函数,f(1-x2)是增函数,
t≥0时,1≥x≥-1,
t=1-x2 在(0,1]上是减函数,f(1-x2)是增函数,
则f(1-x2)是增函数的区间是 (-∞,-1]∪(0,1],
故选 D.
点评:本题考查函数的单调性和奇偶性的应用,对复合函数,只有内层函数和外层函数都是增函数或都是减函数时,它才是增函数.

练习册系列答案
 提分百分百检测卷系列答案
提分百分百检测卷系列答案 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案
相关题目
若
=b,则a+b=( )
| lim |
| x→1 |
| x+a | |||
|
| A、-2 | B、0 | C、2 | D、4 |
设函数f(x)=
x3-mx2+(m2-4)x,x∈R,当m=3时,则曲线y=f(x)在点(2,f(2))处的切线方程为( )
| 1 |
| 3 |
| A、9x+3y-20=0 |
| B、9x+3y-2=0 |
| C、9x+3y-10=0 |
| D、9x+3y+20=0 |
直线l与平面a内的两条直线都垂直,则直线l与平面a的位置关系是( )
| A、平行 | B、垂直 |
| C、在平面a内 | D、无法确定 |
a≥0,b≥0,a+b=1,且x1,x2为正数,y1=ax1+bx2,y2=bx1+ax2,则y1y2与x1x2的大小关系是( )
| A、y1y2≥x1x2 |
| B、y1y2≤x1x2 |
| C、y1y2>x1x2 |
| D、y1y2<x1x2 |
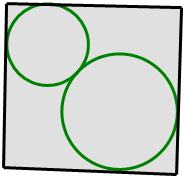 如图,在单位正方形内作两个互相外切的圆,同时每一个圆又与正方形的两相邻边相切,记其中一个圆的半径为x,两圆的面积之和为S,将S表示为x的函数,求函数S=f(x)的解析式及f(x)的值域.
如图,在单位正方形内作两个互相外切的圆,同时每一个圆又与正方形的两相邻边相切,记其中一个圆的半径为x,两圆的面积之和为S,将S表示为x的函数,求函数S=f(x)的解析式及f(x)的值域. 有两项
有两项 和
和 ,满足
,满足 ,则该数列前
,则该数列前 项之和为 ( )
项之和为 ( ) B
B  C
C  D
D 