题目内容
设ξ的概率密度函数为f(x)=
e-
,则下列结论错误的是( )
| 1 | ||
|
| (x-1)2 |
| 2 |
| A、p(ξ<1)=p(ξ>1) |
| B、p(-1≤ξ≤1)=p(-1<ξ<1) |
| C、f(x)的渐近线是x=0 |
| D、η=ξ-1~N(0,1) |
考点:正态分布曲线的特点及曲线所表示的意义
专题:常规题型
分析:根据变量的概率密度函数解析式,得到这个变量的性质,根据样本的均值知道A正确,根据变量对应的概率等于对应的面积,知B正确,根据正态曲线是与X轴无限接近的,得到渐近线是x轴,知道C是一个错误说法.
解答:
解:∵ξ的概率密度函数为f(x)=
e-
,
∴μ=1,
∴p(ξ<1)=p(ξ>1),p(-1≤ξ≤1)=p(-1<ξ<1),
当变量ξ符合正态分布时,ξ与一个常数的加减运算也符合正态分布,
f(x)的渐近线是y=0.
故选C.
| 1 | ||
|
| (x-1)2 |
| 2 |
∴μ=1,
∴p(ξ<1)=p(ξ>1),p(-1≤ξ≤1)=p(-1<ξ<1),
当变量ξ符合正态分布时,ξ与一个常数的加减运算也符合正态分布,
f(x)的渐近线是y=0.
故选C.
点评:本题考查符合正态分布的变量的概率密度函数,考查正态曲线的特点及曲线所表示的意义,是一个基础题,题目不需要计算,只要了解正态曲线的性质,就可以做出结论.

练习册系列答案
 一线名师提优试卷系列答案
一线名师提优试卷系列答案
相关题目
设函数f(x)=
x3-mx2+(m2-4)x,x∈R,当m=3时,则曲线y=f(x)在点(2,f(2))处的切线方程为( )
| 1 |
| 3 |
| A、9x+3y-20=0 |
| B、9x+3y-2=0 |
| C、9x+3y-10=0 |
| D、9x+3y+20=0 |
直线l与平面a内的两条直线都垂直,则直线l与平面a的位置关系是( )
| A、平行 | B、垂直 |
| C、在平面a内 | D、无法确定 |


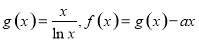 .
.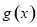 的单调区间;
的单调区间; 上是减函数,求实数a的最小值;
上是减函数,求实数a的最小值; ,使
,使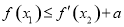 成立,求实数a的取值范围.
成立,求实数a的取值范围.