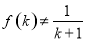题目内容
(本题满分12分)已知函数 =sin(2x+
=sin(2x+ )+ cos 2x.
)+ cos 2x.
(1)求函数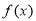 的单调递增区间。
的单调递增区间。
(2)在△ABC中,内角A、B、C的对边分别为a、b、c,已知f(A)=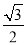 ,a=2,B=
,a=2,B=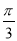 ,求△ABC的面积.
,求△ABC的面积.
(1)f(x)的单调递增区间为: ;(2)
;(2)
【解析】
试题分析:(1)【解析】
=
=
= 3分
3分
令
解得 ,
,
f(x)的单调递增区间为: 6分
6分
(2)由 ,
,
又
因此 ,解得:
,解得: 8分
8分
由正弦定理 ,得
,得 ,
,
又由 可得:
可得: 10分
10分
故 12分
12分
考点:本题考查两角和与差的三角函数,正弦函数的图象和性质,正弦定理

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案
相关题目
a≥0,b≥0,a+b=1,且x1,x2为正数,y1=ax1+bx2,y2=bx1+ax2,则y1y2与x1x2的大小关系是( )
| A、y1y2≥x1x2 |
| B、y1y2≤x1x2 |
| C、y1y2>x1x2 |
| D、y1y2<x1x2 |
 、
、 满足
满足 ,则
,则 的最小值为( )
的最小值为( ) (C)
(C) (D)
(D)
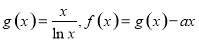 .
.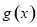 的单调区间;
的单调区间; 上是减函数,求实数a的最小值;
上是减函数,求实数a的最小值; ,使
,使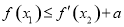 成立,求实数a的取值范围.
成立,求实数a的取值范围.
 有两项
有两项 和
和 ,满足
,满足 ,则该数列前
,则该数列前 项之和为 ( )
项之和为 ( ) B
B  C
C  D
D 
 的公差
的公差 ,且
,且 成等比数列,若
成等比数列,若 是数列
是数列 项的和,则
项的和,则 的最小值为( )
的最小值为( ) D.
D.
 是定义域为正整数集的函数,具有如下性质:对于定义域内任意的
是定义域为正整数集的函数,具有如下性质:对于定义域内任意的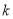 ,如果
,如果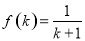 成立,则
成立,则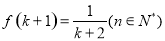 成立,那么下列命题正确的是___
成立,那么下列命题正确的是___ 成立,则对于任意
成立,则对于任意 ,均有
,均有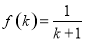
 成立,则对于任意
成立,则对于任意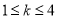 ,均有
,均有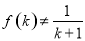
 成立,则对于任意
成立,则对于任意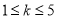 ,均有
,均有