题目内容
解方程：
+
=
．
| C | x-2 x+2 |
| C | x-3 x+2 |
| 1 |
| 10 |
| A | 3 x+3 |
考点：组合及组合数公式
专题：计算题
分析：利用排列和数组合数公式，灵活化简求得答案．
解答：
解：∵
+
=
，
∴
+
=
•
，
∴
+
=
•
，
∴
+
=
，
∴5x（x-1）+x（x-1）（x-2）=12（x+3），
∴x（x-1）（5+x-2）-12（x+3）=0，
∴x（x-1）（x+3）-12（x+3）=0，
∴（x+3）（x-x-12）=0，
∴（x+3）（x+3）（x-4）=0，
解得，x=-3（不能为负数舍去），或x=4．
∴x=4．
| C | x-2 x+2 |
| C | x-3 x+2 |
| 1 |
| 10 |
| A | 3 x+3 |
∴
| (x+2)! |
| (x-2)!•[(x+2)-(x-2)]! |
| (x+2)! |
| (x-3)!•[(x+2)-(x-3)]! |
| 1 |
| 10 |
| (x+3)! |
| (x+3-3)! |
∴
| (x+2)! |
| 4!•(x-2)(x-3)! |
| (x+2)! |
| 5!•(x-3)! |
| 1 |
| 10 |
| (x+3)(x+2)! |
| x(x-1)(x-2)(x-3)! |
∴
| 1 |
| 24(x-2) |
| 1 |
| 120 |
| x+3 |
| 10x(x-1)(x-2) |
∴5x（x-1）+x（x-1）（x-2）=12（x+3），
∴x（x-1）（5+x-2）-12（x+3）=0，
∴x（x-1）（x+3）-12（x+3）=0，
∴（x+3）（x-x-12）=0，
∴（x+3）（x+3）（x-4）=0，
解得，x=-3（不能为负数舍去），或x=4．
∴x=4．
点评：本题在解方程的过程中要合理的把阶乘经行分解，约分化简，做题要仔细认真！
练习册系列答案
相关题目
已知f（x）是定义在R上的奇函数，当x＞0时，f（x）=2+f（
）log2x，则f（-2）=（ ）
| 1 |
| 2 |
| A、1 | B、3 | C、-1 | D、-3 |
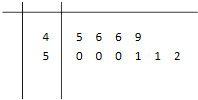一批食品，每袋的标准重量是50g，为了了解这批食品的实际重量情况，从中随机抽取10袋食品，称出各袋的重量（单位：g），并得到其茎叶图（如图）．