题目内容
已知函数f(x)=x2+2x+3,当x∈[t,t+1],f(x)≥t恒成立,求t的取值范围.
考点:二次函数在闭区间上的最值
专题:函数的性质及应用
分析:由题意可得t小于或等于f(x)在[t,t+1]上的最小值,分t≥-1、t<-1<t+1、t+1≤-1 三种情况,分别求得f(x)的最小值,从而求得t的范围.
解答:
解:∵函数f(x)=x2+2x+3=(x+1)2+2,当x∈[t,t+1],f(x)≥t恒成立,
故t小于或等于f(x)在[t,t+1]上的最小值.
当t≥-1时,f(x)在[t,t+1]上是增函数,最小值为f(t)=t2+2t+3,
由
求得t≥-1.
当t<-1<t+1时,f(x)的最小值为f(-1)=2,
由
,求得-2<t<-1.
当t+1≤-1,f(x)在[t,t+1]上是减函数,f(x)的最小值为f(t+1)=t2+4t+6,
由
,求得 t≤-2.
综上可得t的范围是R.
故t小于或等于f(x)在[t,t+1]上的最小值.
当t≥-1时,f(x)在[t,t+1]上是增函数,最小值为f(t)=t2+2t+3,
由
|
当t<-1<t+1时,f(x)的最小值为f(-1)=2,
由
|
当t+1≤-1,f(x)在[t,t+1]上是减函数,f(x)的最小值为f(t+1)=t2+4t+6,
由
|
综上可得t的范围是R.
点评:本题主要考查求二次函数在闭区间上的最值,体现了分类讨论的数学思想,属于中档题.

练习册系列答案
 作业辅导系列答案
作业辅导系列答案 同步学典一课多练系列答案
同步学典一课多练系列答案 经典密卷系列答案
经典密卷系列答案
相关题目
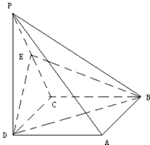 如图,在四棱锥P-ABCD中,底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC=2,E是PC的中点.
如图,在四棱锥P-ABCD中,底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC=2,E是PC的中点.