题目内容
设命题p:|x-3|+|x+1|≤6,命题q:|x+a|>x+a.
(1)求命题p,q对应不等式的解集A,B;
(2)若p⇒q为真命题,q⇒p为假命题,求实数a的取值范围.
(1)求命题p,q对应不等式的解集A,B;
(2)若p⇒q为真命题,q⇒p为假命题,求实数a的取值范围.
考点:必要条件、充分条件与充要条件的判断
专题:直线与圆
分析:(1)对于命题p:由于|x-3|+|x+1|=
,可得|x-3|+|x+1|≤6的解集为[-2,4]=A.
对于命题q:由于|x+a|>x+a.可得x+a<0,可得|x+a|>x+a的解集为(-∞,-a)=B.
(2)由于p⇒q为真命题,q⇒p为假命题,可得p是q的充分不必要条件,A?B,即可得出.
|
对于命题q:由于|x+a|>x+a.可得x+a<0,可得|x+a|>x+a的解集为(-∞,-a)=B.
(2)由于p⇒q为真命题,q⇒p为假命题,可得p是q的充分不必要条件,A?B,即可得出.
解答:
解:(1)对于命题p:∵|x-3|+|x+1|=
,
∴当x>3时,由2x-2≤6,解得3<x≤4;
当3≥x≥-1时,由4≤6,解得-1≤x≤3;
当x<-1时,由-2x+2≤6,解得-2≤x<-1.
综上可得:|x-3|+|x+1|≤6的解集为[-2,4]=A.
对于命题q:∵|x+a|>x+a.∴x+a<0,解得x<-a.
∴|x+a|>x+a的解集为(-∞,-a)=B.
(2)∵p⇒q为真命题,q⇒p为假命题,
∴p是q的充分不必要条件,
∴A?B,
∴4<-a,
解得a<-4.
|
∴当x>3时,由2x-2≤6,解得3<x≤4;
当3≥x≥-1时,由4≤6,解得-1≤x≤3;
当x<-1时,由-2x+2≤6,解得-2≤x<-1.
综上可得:|x-3|+|x+1|≤6的解集为[-2,4]=A.
对于命题q:∵|x+a|>x+a.∴x+a<0,解得x<-a.
∴|x+a|>x+a的解集为(-∞,-a)=B.
(2)∵p⇒q为真命题,q⇒p为假命题,
∴p是q的充分不必要条件,
∴A?B,
∴4<-a,
解得a<-4.
点评:本题考查了绝对值不等式的解法、分类讨论方法、简易逻辑的有关知识,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
函数y=-x2的单调区间为( )
| A、(-∞,0)为减区间 |
| B、(0,+∞)为增区间 |
| C、(-∞,+∞) |
| D、(-∞,0)为增区间,(0,+∞)为减区间 |
已知定义在R上的奇函数f(x)和偶函数g(x)满足f(x)+g(x)=ax-a-x+2(a>0,且a≠1),若g(2013)=a,则f(-2013)=( )
| A、2 |
| B、2-2013-22013 |
| C、22013-2-2013 |
| D、a2 |
某中学高三(1)班有学生x人,现按座位号的编号采用系统抽样的方法选取5名同学参加一项活动,已知座位号为5号、16号、27号、38号、49号的同学均被选出,则该班的学生人数x的值不可能的是( )
| A、55 | B、57 | C、59 | D、61 |
一个K进制的三位数与某六进制的二位数等值,则K不可能是( )
| A、3 | B、4 | C、5 | D、7 |
已知X的分布列是
设Y=2X+3,则E(X)的值为( )
| X | -1 | 0 | 1 | ||||||
| P |
|
|
|
A、
| ||
| B、4 | ||
| C、-1 | ||
| D、1 |
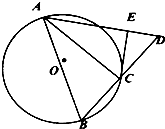 如图,AB是圆O的弦,点C在圆O上,延长BC到D,使BC=CD,AB=AD.
如图,AB是圆O的弦,点C在圆O上,延长BC到D,使BC=CD,AB=AD.