题目内容
已知π<θ<3π,则
化简为( )
|
A、sin
| ||
B、cos
| ||
C、-sin
| ||
D、-cos
|
考点:二倍角的余弦
专题:三角函数的求值
分析:由二倍角的余弦公式将原式化简,再确定
的取值范围,即可确定答案.
| θ |
| 2 |
解答:
解:∵cosθ=2cos2
-1.
∴
=|cos
|.
又∵π<θ<3π,
<
<
,
故:|cos
|=-cos
.
故选:D.
| θ |
| 2 |
∴
|
| θ |
| 2 |
又∵π<θ<3π,
| π |
| 2 |
| θ |
| 2 |
| 3π |
| 2 |
故:|cos
| θ |
| 2 |
| θ |
| 2 |
故选:D.
点评:本题主要考察了二倍角的余弦公式的应用,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
(理)直平行六面体ABCD-A1B1C1D1的棱长均为2,∠BAD=60°,则对角线A1C与侧面D1C1CD所成角的正弦值为( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
{an}和{bn},其前n项和分别为Sn,Tn,且
=
,则
等于( )
| Sn |
| Tn |
| 7n+2 |
| n+3 |
| a2+a20 |
| b2+b20 |
A、
| ||
B、
| ||
C、
| ||
D、
|
已知{an}是等差数列,a1+a2=4,a7+a8=28,则该数列前8项和S8等于( )
| A、72 | B、64 |
| C、100 | D、120 |
 如图,已知平行四边形ABCD中,E、F分别为边AB、AD上的点,EF与对角线AC交于点P.若
如图,已知平行四边形ABCD中,E、F分别为边AB、AD上的点,EF与对角线AC交于点P.若| AE |
| EB |
| a |
| b |
| AF |
| FD |
| m |
| n |
| AP |
| PC |
A、
| ||
B、
| ||
C、
| ||
D、
|
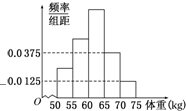 如图是某学校抽取的学生体重的频率分布直方图,已知图中从左到右的前3个小组的频率之比为1:2:3,第2小组的频数为10,则抽取的学生人数为( )
如图是某学校抽取的学生体重的频率分布直方图,已知图中从左到右的前3个小组的频率之比为1:2:3,第2小组的频数为10,则抽取的学生人数为( )