题目内容
解不等式:2|x|+2x≥2
.
| 2 |
考点:指、对数不等式的解法
专题:不等式的解法及应用
分析:当x≥0时,原不等式可化为2•2x≥2
,由指数函数的单调性可得;当x<0时,原不等式可化为2-x+2x≥2
,解关于2x的一元二次不等式可得.
| 2 |
| 2 |
解答:
解:当x≥0时,原不等式可化为2•2x≥2
,
即2x+1≥2
,∴x+1≥
,解得x≥
,
∴此时原不等式的解集为:{x|x≥
};
当x<0时,原不等式可化为2-x+2x≥2
,
变形可得(2x)2-2
•2x-1≥0,
解得x≥
+
,或x≤
-
∴此时原不等式的解集为:{x|x≤
-
}
| 2 |
即2x+1≥2
| 3 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
∴此时原不等式的解集为:{x|x≥
| 1 |
| 2 |
当x<0时,原不等式可化为2-x+2x≥2
| 2 |
变形可得(2x)2-2
| 2 |
解得x≥
| 2 |
| 3 |
| 2 |
| 3 |
∴此时原不等式的解集为:{x|x≤
| 2 |
| 3 |
点评:本题考查指数不等式的解法,去绝对值是解决问题的关键,属基础题.

练习册系列答案
相关题目
下列求导函数运算正确的是( )
A、(x+
| ||||
B、(
| ||||
| C、[(3+x2)(2-x3)]′=2x(2-x3)-3x2(3+x2) | ||||
| D、(x2•cosx)′=2x•cosx+x2•sinx |
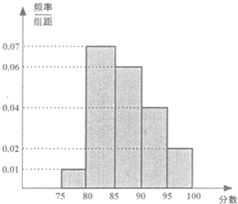 一企业某次招聘新员工分笔试和面试两部分,人力资源部经理把参加笔试的40名学生的成绩分组:第1组[75,80),第2组[80,85),第3组[85,90),第4组[90,95),第5组[95,100),得到频率分布直方图如图所示.
一企业某次招聘新员工分笔试和面试两部分,人力资源部经理把参加笔试的40名学生的成绩分组:第1组[75,80),第2组[80,85),第3组[85,90),第4组[90,95),第5组[95,100),得到频率分布直方图如图所示.