题目内容
已知全集U=R,集合A={x|1≤x<5},B={x|2<x<8}.
(1)求A∪B,(∁UA)∩B;
(2)若C={x|a<x≤a+3},且C∩A=C,求a的取值范围.
(1)求A∪B,(∁UA)∩B;
(2)若C={x|a<x≤a+3},且C∩A=C,求a的取值范围.
考点:交、并、补集的混合运算
专题:集合
分析:(1)由并集的运算求出A∪B,由补集的运算求出∁UA,再由交集的运算求出(∁UA)∩B;
(2)由C∩A=C得C⊆A,由子集的额定义列出关于a的不等式组,求出a的取值范围.
(2)由C∩A=C得C⊆A,由子集的额定义列出关于a的不等式组,求出a的取值范围.
解答:
解:(1)因为集合A={x|1≤x<5},B={x|2<x<8},
所以A∪B={x|1≤x<8},∁UA={x|x<1或x≥5},
(∁UA)∩B={x|5≤x<8},
(2)由C∩A=C得,C⊆A,
所以
,解得1≤a<2,
则a的取值范围是[1,2).
所以A∪B={x|1≤x<8},∁UA={x|x<1或x≥5},
(∁UA)∩B={x|5≤x<8},
(2)由C∩A=C得,C⊆A,
所以
|
则a的取值范围是[1,2).
点评:本题考查交、并、补集的混合运算,以及子集的定义,注意端点处是否取到等号.

练习册系列答案
相关题目
已知
,
满足:|
|=3,|
|=2,则|
+
|=4,则|
-
|=( )
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
A、
| ||
B、
| ||
| C、3 | ||
D、
|
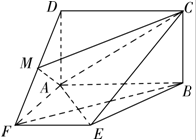 如图,四边形ABCD是矩形,BC⊥平面ABEF,四边形ABEF是梯形,∠EFA=∠FAB=90°,EF=FA=AD=1,AB=2,点M是DF的中点.
如图,四边形ABCD是矩形,BC⊥平面ABEF,四边形ABEF是梯形,∠EFA=∠FAB=90°,EF=FA=AD=1,AB=2,点M是DF的中点.