题目内容
在三棱柱ABC-A1B1C1中,底面ABC为正△,侧棱A1A⊥面ABC,若AB=AA1,则异面直线A1B与AC所成的角的余弦值等于 .
考点:异面直线及其所成的角
专题:计算题,作图题,空间位置关系与距离
分析:由题意作图如右图,连结BC1,取A1C1的中点D,连结BD,从而可知∠BA1C1是异面直线A1B与AC所成的角,求得cos∠BA1C1=
=
.
| ||
|
| ||
| 4 |
解答:
 解:由题意作图如右图,
解:由题意作图如右图,
连结BC1,取A1C1的中点D,连结BD,
则由题意可得,
A1C1∥AC,
故∠BA1C1是异面直线A1B与AC所成的角,
又∵A1B=
AB,BC1=
AB,A1C1=AB,
故cos∠BA1C1=
=
,
故答案为:
.
 解:由题意作图如右图,
解:由题意作图如右图,连结BC1,取A1C1的中点D,连结BD,
则由题意可得,
A1C1∥AC,
故∠BA1C1是异面直线A1B与AC所成的角,
又∵A1B=
| 2 |
| 2 |
故cos∠BA1C1=
| ||
|
=
| ||
| 4 |
故答案为:
| ||
| 4 |
点评:本题考查了学生的空间想象力及异面直线所成角的作法,属于中档题.

练习册系列答案
 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案
相关题目
已知△ABC的三内角的度数成等差数列,则其中间一项的度数是( )
| A、30° | B、60° |
| C、90° | D、120° |
已知命题 p:?x∈R,cosx≤1,则( )
| A、¬p:?x0∈R,cosx0≥1 |
| B、¬p:?x∈R,cosx≥1 |
| C、¬p:?x∈R,cosx>1 |
| D、¬p:?x0∈R,cosx0>1 |

 (文科)如图,三棱柱ABC-A1B1C1D1,中,侧面BB1C1C为菱形,B1C的中点为O,且AO⊥平面BB1C1C.
(文科)如图,三棱柱ABC-A1B1C1D1,中,侧面BB1C1C为菱形,B1C的中点为O,且AO⊥平面BB1C1C.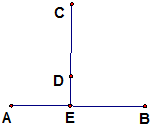 如图,某山区的两个工厂A、B直线距离14km,工厂C距A、B直线距离都是25km,E为线段AB的中点,在线段CE上选建变电站D,并从点D处铺设到工厂A,B,C的输电线DA,DB,DC.
如图,某山区的两个工厂A、B直线距离14km,工厂C距A、B直线距离都是25km,E为线段AB的中点,在线段CE上选建变电站D,并从点D处铺设到工厂A,B,C的输电线DA,DB,DC.