题目内容
已知双曲线C：
-
=1（a＞0，b＞0）的离心率e=
，经过A（a，0），B（0，-b）两点的直线l与原点的距离d=
（1）求双曲线C的方程；
（2）直线y=kx+5与双曲线C交于M，N两点，若|BM|=|BN|，求斜率k的值．
| x2 |
| a2 |
| y2 |
| b2 |
2
| ||
| 3 |
| ||
| 2 |
（1）求双曲线C的方程；
（2）直线y=kx+5与双曲线C交于M，N两点，若|BM|=|BN|，求斜率k的值．
考点：直线与圆锥曲线的关系,椭圆的标准方程
专题：计算题,圆锥曲线中的最值与范围问题
分析：（1）由题意可得，
，从而解出双曲线C的方程；
（2）由题意可得
，即（1-3k2）x2-30kx-78=0，从而得到中点E（
，
），从而得到k•
=-1，从而求解．
|
（2）由题意可得
|
| 15k |
| 1-3k2 |
| 5 |
| 1-3k2 |
| 2-k2 |
| 5k |
解答：
解：（1）由题意可得，
，
解得，a=
，b=1，c=2；
故双曲线C的方程为：
-y2=1；
（2）由题意可得
，
即（1-3k2）x2-30kx-78=0，
设MN的中点为E，
则E（
，
），
则kEB=
，
则k•
=-1，
解得，k=±
．
|
解得，a=
| 3 |
故双曲线C的方程为：
| x2 |
| 3 |
（2）由题意可得
|
即（1-3k2）x2-30kx-78=0，
设MN的中点为E，
则E（
| 15k |
| 1-3k2 |
| 5 |
| 1-3k2 |
则kEB=
| 2-k2 |
| 5k |
则k•
| 2-k2 |
| 5k |
解得，k=±
| 7 |
点评：本题考查了圆锥曲线的定义及性质，同时考查了直线与圆锥曲线的关系，属于难题．
练习册系列答案
阅读快车系列答案
相关题目
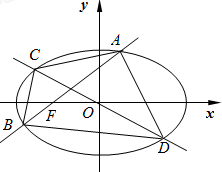如图，已知椭圆E：
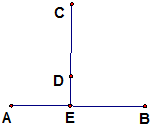如图，某山区的两个工厂A、B直线距离14km，工厂C距A、B直线距离都是25km，E为线段AB的中点，在线段CE上选建变电站D，并从点D处铺设到工厂A，B，C的输电线DA，DB，DC．
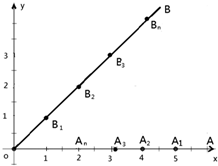平面直角坐标系中，O为原点，射线OA与x轴正半轴重合，射线OB是第一象限角平分线．在OA上有点列A1，A2，A3，…，An，…，在OB上有点列B1，B2，B3，…，Bn，…已知