题目内容
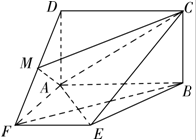 如图,四边形ABCD是矩形,BC⊥平面ABEF,四边形ABEF是梯形,∠EFA=∠FAB=90°,EF=FA=AD=1,AB=2,点M是DF的中点.
如图,四边形ABCD是矩形,BC⊥平面ABEF,四边形ABEF是梯形,∠EFA=∠FAB=90°,EF=FA=AD=1,AB=2,点M是DF的中点.(Ⅰ)求证:BF∥平面AMC,
(Ⅱ)求二面角B-AC-E的余弦值.
考点:二面角的平面角及求法,直线与平面平行的判定
专题:空间位置关系与距离,空间角
分析:(Ⅰ)通过三角形的中位线得到线线平行,进一步利用线面平行的判定得到结论.
(Ⅱ)首先做出二面角的平面角,进一步利用相关的三角形相似,线面垂直的性质求得相关的线段长,最后求得结论.
(Ⅱ)首先做出二面角的平面角,进一步利用相关的三角形相似,线面垂直的性质求得相关的线段长,最后求得结论.
解答:
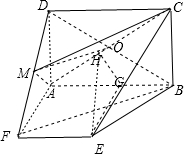
(Ⅰ)证明:连接AC,BD交与点O,连接OM
由于:M、O是FD、AC的中点,
所以:OM∥FB
BF?平面MAC,OM?平面MAC
所以:BF∥平面AMC.
(Ⅱ)在平面ABEF中,过E点做EG⊥AD于G,过G做GH⊥AC于H,连接EH,
所以:∠EHG是二面角B-AC-E的平面角.
由于:四边形ABCD是矩形,BC⊥平面ABEF,四边形ABEF是梯形,
∠EFA=∠FAB=90°,EF=FA=AD=1,AB=2,
所以:利用△AGH∽△ACB
解得:GH=
EG=1
在Rt△EGH中,tan∠EHG=
所以:cos∠EHG=
由于:M、O是FD、AC的中点,
所以:OM∥FB
BF?平面MAC,OM?平面MAC
所以:BF∥平面AMC.
(Ⅱ)在平面ABEF中,过E点做EG⊥AD于G,过G做GH⊥AC于H,连接EH,
所以:∠EHG是二面角B-AC-E的平面角.
由于:四边形ABCD是矩形,BC⊥平面ABEF,四边形ABEF是梯形,
∠EFA=∠FAB=90°,EF=FA=AD=1,AB=2,
所以:利用△AGH∽△ACB
解得:GH=
| ||
| 5 |
EG=1
在Rt△EGH中,tan∠EHG=
| 5 |
所以:cos∠EHG=
| ||
| 30 |

点评:本题考查的知识要点:线面平行的判定,线面垂直的性质,二面角平面角的做法,三角形的相似,及相关的运算,属于基础题型.

练习册系列答案
相关题目
已知y=f(x)是定义在R上的奇函数,当x≥0时,f(x)=x(x-2),则当x<0时f(x)上的表达式为( )
| A、y=x(x-2) |
| B、y=x(x+2) |
| C、y=-x(x-2) |
| D、y=-x(x+2) |
已知集合A={x|0<x<2},集合B={x|1<x≤3},则A∪B=( )
| A、A={x|0<x<3} |
| B、B={x|0<x≤3} |
| C、B={x|1<x<2} |
| D、B={x|0<x<3} |
已知=
(1,2),
=(0,1),
=(-2,k),若(
+2
)⊥
,则k=( )
| a |
| b |
| c |
| a |
| b |
| c |
A、-
| ||
| B、-2 | ||
| C、2 | ||
D、
|
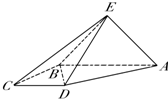 如图,四棱锥E-ABCD中,面ABE⊥面ABCD,侧面ABE是等腰直角三角形,EA⊥EB,且AB∥CD,AB⊥BC,AB=2CD=2BC=2.
如图,四棱锥E-ABCD中,面ABE⊥面ABCD,侧面ABE是等腰直角三角形,EA⊥EB,且AB∥CD,AB⊥BC,AB=2CD=2BC=2.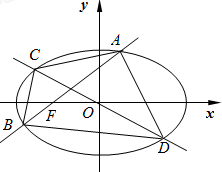 如图,已知椭圆E:
如图,已知椭圆E: