题目内容

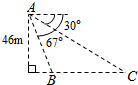如图，从气球A上测得正前方的河流的两岸B，C的俯角分别为67°，30°，此时气球的高是46m，则河流的宽度BC约等于
 
m．（用四舍五入法将结果精确到个位．参考数据：sin67°≈0.92，cos67°≈0.39，sin37°≈0.60，cos37°≈0.80，
3
≈1.73）
考点：余弦定理的应用,正弦定理,正弦定理的应用
专题：应用题,解三角形
分析：过A点作AD垂直于CB的延长线，垂足为D，分别在Rt△ACD、Rt△ABD中利用三角函数的定义，算出CD、BD的长，从而可得BC，即为河流在B、C两地的宽度．
解答： 解：过A点作AD垂直于CB的延长线，垂足为D，
则Rt△ACD中，∠C=30°，AD=46m，
AB=
46
sin67°
，根据正弦定理，
AB
sin30°
=
BC
sin37°
，
得BC=
ABsin37°
sin30°
=46×
sin37°
sin67°sin30°
=60m．
故答案为：60m．
点评：本题给出实际应用问题，求河流在B、C两地的宽度，着重考查了三角函数的定义、正余弦定理解三角形的知识，属于中档题．
练习册系列答案
相关题目
已知函数f（x）=
a•2x  ，x≥0
2-x  ，x＜0
（a∈R），若f[f（-1）]=1，则a=（　　）
A、
1
4
B、
1
2
C、1
D、2
某市为了了解本市2014届高三学生的数学毕业考试成绩（满分100分），随机抽取45名学生进行调查，得到茎叶图如图所示，将得分不低于80的称为“优秀”．
不优秀 优秀 合计
男
女
合计
①根据已知条件，完成下面的2×2列联表，据此资料你能否有90%的把握认为学生的数学成绩与性别有关；
②将上述调查所得到的频率视为概率，现从该市参加学业考试的女学生中随机抽取4名学生，记被抽取的4名学生成绩优秀的人数记为ξ，求ξ的分布列及其数学期望．
参考公式：K2=
n(ad-bc)2
(a+b)(c+d)(a+c)(b+d)
，n=a+b+c+d．
P（K2≥k0） 0.10 0.01 0.005 0.001
k0 2，706 6.635 7.879 10.828
已知双曲线
x2
a2
-
y2
b2
=1（a＞0，b＞0）的焦距为2c，右顶点为A，抛物线x2=2py（p＞0）的焦点为F，若双曲线截抛物线的准线所得线段长为2c，且|FA|=c，则双曲线的渐近线方程为
 
．
若曲线y=e-x上点P的切线平行于直线2x+y+1=0，则点P的坐标是
 
．
若函数f（x）=ax3+3x2-x恰好有三个单调区间，那么a的取值范围是
 
．
若关于x的不等式|ax-2|＜3的解集为{x|-
5
3
＜x＜
1
3
}，则a=
 
．
设函数f（x）=
x2+x， x＜0
-x2，  x≥0
，若f（f（a））≤2，则实数a的取值范围是
 
．
钝角三角形ABC的面积是
1
2
，AB=1，BC=
2
，则AC=（　　）
A、5
B、
5
C、2
D、1

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网