题目内容
已知函数f（x）=
（a∈R），若f[f（-1）]=1，则a=（ ）
|
A、
| ||
B、
| ||
| C、1 | ||
| D、2 |
考点：分段函数的应用
专题：函数的性质及应用
分析：根据条件代入计算即可．
解答：
解：∵f[f（-1）]=1，
∴f[f（-1）]=f（2-（-1））=f（2）=a•22=4a=1
∴a=
．
故选：A．
∴f[f（-1）]=f（2-（-1））=f（2）=a•22=4a=1
∴a=
| 1 |
| 4 |
故选：A．
点评：本题主要考查了求函数值的问题，关键是分清需要代入到那一个解析式中，属于基础题．
练习册系列答案
相关题目
设四边形ABCD的两条对角线为AC，BD，则“四边形ABCD为菱形”是“AC⊥BD”的（ ）
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充分必要条件 |
| D、既不充分也不必要条件 |
若二项式（2x+
）7的展开式中
的系数是84，则实数a=（ ）
| a |
| x |
| 1 |
| x3 |
| A、2 | ||||
B、
| ||||
| C、1 | ||||
D、
|
已知f（x）是定义在R上的奇函数，当x≥0时，f（x）=x2-3x，则函数g（x）=f（x）-x+3的零点的集合为（ ）
| A、{1，3} | ||
| B、{-3，-1，1，3} | ||
C、{2-
| ||
D、{-2-
|
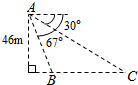如图，从气球A上测得正前方的河流的两岸B，C的俯角分别为67°，30°，此时气球的高是46m，则河流的宽度BC约等于