题目内容
钝角三角形ABC的面积是
,AB=1,BC=
,则AC=( )
| 1 |
| 2 |
| 2 |
| A、5 | ||
B、
| ||
| C、2 | ||
| D、1 |
考点:余弦定理
专题:三角函数的求值
分析:利用三角形面积公式列出关系式,将已知面积,AB,BC的值代入求出sinB的值,分两种情况考虑:当B为钝角时;当B为锐角时,利用同角三角函数间的基本关系求出cosB的值,利用余弦定理求出AC的值即可.
解答:
解:∵钝角三角形ABC的面积是
,AB=c=1,BC=a=
,
∴S=
acsinB=
,即sinB=
,
当B为钝角时,cosB=-
=-
,
利用余弦定理得:AC2=AB2+BC2-2AB•BC•cosB=1+2+2=5,即AC=
,
当B为锐角时,cosB=
=
,
利用余弦定理得:AC2=AB2+BC2-2AB•BC•cosB=1+2-2=1,即AC=1,
此时AB2+AC2=BC2,即△ABC为直角三角形,不合题意,舍去,
则AC=
.
故选:B.
| 1 |
| 2 |
| 2 |
∴S=
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
当B为钝角时,cosB=-
| 1-sin2B |
| ||
| 2 |
利用余弦定理得:AC2=AB2+BC2-2AB•BC•cosB=1+2+2=5,即AC=
| 5 |
当B为锐角时,cosB=
| 1-sin2B |
| ||
| 2 |
利用余弦定理得:AC2=AB2+BC2-2AB•BC•cosB=1+2-2=1,即AC=1,
此时AB2+AC2=BC2,即△ABC为直角三角形,不合题意,舍去,
则AC=
| 5 |
故选:B.
点评:此题考查了余弦定理,三角形面积公式,以及同角三角函数间的基本关系,熟练掌握余弦定理是解本题的关键.

练习册系列答案
相关题目
执行如图所示的程序框图,若输入的x,t均为2,则输出的S=( )


| A、4 | B、5 | C、6 | D、7 |
记max{x,y}=
,min{x,y}=
,设
,
为平面向量,则( )
|
|
| a |
| b |
A、min{|
| ||||||||||||
B、min{|
| ||||||||||||
C、max{|
| ||||||||||||
D、max{|
|
设向量
,
满足|
+
|=
,|
-
|=
,则
•
=( )
| a |
| b |
| a |
| b |
| 10 |
| a |
| b |
| 6 |
| a |
| b |
| A、1 | B、2 | C、3 | D、5 |
设集合S={x|x≥2},T={x|x≤5},则S∩T=( )
| A、(-∞,5] |
| B、[2,+∞) |
| C、(2,5) |
| D、[2,5] |
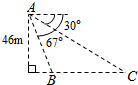 如图,从气球A上测得正前方的河流的两岸B,C的俯角分别为67°,30°,此时气球的高是46m,则河流的宽度BC约等于
如图,从气球A上测得正前方的河流的两岸B,C的俯角分别为67°,30°,此时气球的高是46m,则河流的宽度BC约等于