题目内容
 某市为了了解本市2014届高三学生的数学毕业考试成绩(满分100分),随机抽取45名学生进行调查,得到茎叶图如图所示,将得分不低于80的称为“优秀”.
某市为了了解本市2014届高三学生的数学毕业考试成绩(满分100分),随机抽取45名学生进行调查,得到茎叶图如图所示,将得分不低于80的称为“优秀”.| 不优秀 | 优秀 | 合计 | |
| 男 | |||
| 女 | |||
| 合计 |
②将上述调查所得到的频率视为概率,现从该市参加学业考试的女学生中随机抽取4名学生,记被抽取的4名学生成绩优秀的人数记为ξ,求ξ的分布列及其数学期望.
参考公式:K2=
| n(ad-bc)2 |
| (a+b)(c+d)(a+c)(b+d) |
| P(K2≥k0) | 0.10 | 0.01 | 0.005 | 0.001 |
| k0 | 2,706 | 6.635 | 7.879 | 10.828 |
考点:独立性检验的应用,线性回归方程
专题:综合题,概率与统计
分析:①根据所给的茎叶图得出数据列出列联表,再代入公式计算得出K2,与临界值比较即可得出结论;
②由题意可知:ξ~B(4,
),即可求ξ的分布列及其数学期望.
②由题意可知:ξ~B(4,
| 8 |
| 25 |
解答:
①解:
…(3分)
K2=
=1.5<2.706 …(6分)
∴不能有90%的把握认为学生的数学成绩与性别有关 …(7分)
②由题意可知:ξ~B(4,
),
ξ的分布列
∴Eξ=4×
=
…(12分)
| 不优秀 | 优秀 | 合计 | |
| 男 | 10 | 10 | 20 |
| 女 | 17 | 8 | 25 |
| 合计 | 27 | 18 | 45 |
K2=
| 45×(17×10-10×8)2 |
| 27×18×20×25 |
∴不能有90%的把握认为学生的数学成绩与性别有关 …(7分)
②由题意可知:ξ~B(4,
| 8 |
| 25 |
ξ的分布列
| ξ | 0 | 1 | 2 | 3 | 4 | ||||||||||||||||||||||
| P | (
|
|
|
|
(
|
| 8 |
| 25 |
| 32 |
| 25 |
点评:本题考查独立性检验的运用,考查数据处理能力、运算求解能力和应用意识,考查分布列及其数学期望,属于中档题.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
设四边形ABCD的两条对角线为AC,BD,则“四边形ABCD为菱形”是“AC⊥BD”的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充分必要条件 |
| D、既不充分也不必要条件 |
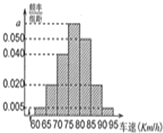 2014年“五一节”期间,高速公路车辆较多,交警部门通过路面监控装置抽样调查某一山区路段汽车行驶速度,采用的方法是:按到达监控点先后顺序,每隔50辆抽取一辆,总共抽取120辆,分别记下其行车速度,将行车速度(km/h)分成七段[60,65),[65,70),[70,75),[75,80),[80,85),[85,90),[90,95)后得到如图所示的频率分布直方图,据图解答下列问题:
2014年“五一节”期间,高速公路车辆较多,交警部门通过路面监控装置抽样调查某一山区路段汽车行驶速度,采用的方法是:按到达监控点先后顺序,每隔50辆抽取一辆,总共抽取120辆,分别记下其行车速度,将行车速度(km/h)分成七段[60,65),[65,70),[70,75),[75,80),[80,85),[85,90),[90,95)后得到如图所示的频率分布直方图,据图解答下列问题: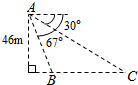 如图,从气球A上测得正前方的河流的两岸B,C的俯角分别为67°,30°,此时气球的高是46m,则河流的宽度BC约等于
如图,从气球A上测得正前方的河流的两岸B,C的俯角分别为67°,30°,此时气球的高是46m,则河流的宽度BC约等于