题目内容
设函数f(x)=
,若f(f(a))≤2,则实数a的取值范围是 .
|
考点:其他不等式的解法
专题:不等式的解法及应用
分析:画出函数f(x)的图象,由 f(f(a))≤2,可得 f(a)≥-2,数形结合求得实数a的取值范围.
解答:
 解:∵函数f(x)=
解:∵函数f(x)=
,它的图象如图所示:
由 f(f(a))≤2,可得 f(a)≥-2.
由f(x)=-2,可得-x2=-2,即x=
,
故当f(f(a))≤2时,则实数a的取值范围是a≤
,
故答案为:(-∞,
].
 解:∵函数f(x)=
解:∵函数f(x)=
|
由 f(f(a))≤2,可得 f(a)≥-2.
由f(x)=-2,可得-x2=-2,即x=
| 2 |
故当f(f(a))≤2时,则实数a的取值范围是a≤
| 2 |
故答案为:(-∞,
| 2 |
点评:本题主要考查分段z函数的应用,其它不等式的解法,体现了数形结合的数学思想,属于中档题.

练习册系列答案
相关题目
执行如图所示的程序框图,若输入的x,t均为2,则输出的S=( )


| A、4 | B、5 | C、6 | D、7 |
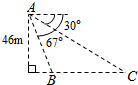 如图,从气球A上测得正前方的河流的两岸B,C的俯角分别为67°,30°,此时气球的高是46m,则河流的宽度BC约等于
如图,从气球A上测得正前方的河流的两岸B,C的俯角分别为67°,30°,此时气球的高是46m,则河流的宽度BC约等于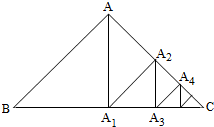 如图,在等腰直角三角形ABC中,斜边BC=2
如图,在等腰直角三角形ABC中,斜边BC=2