题目内容
已知双曲线
-
=1(a>0,b>0)的焦距为2c,右顶点为A,抛物线x2=2py(p>0)的焦点为F,若双曲线截抛物线的准线所得线段长为2c,且|FA|=c,则双曲线的渐近线方程为 .
| x2 |
| a2 |
| y2 |
| b2 |
考点:双曲线的简单性质
专题:圆锥曲线的定义、性质与方程
分析:求出双曲线的右顶点A(a,0),拋物线x2=2py(p>0)的焦点及准线方程,根据已知条件得出a2+
=c2①及
=2c②,求出a=b,得双曲线的渐近线方程为:y=±x.
| p2 |
| 4 |
| a |
| b |
| 4b2+p 2 |
解答:
解:∵右顶点为A,
∴A(a,0),
∵F为抛物线x2=2py(p>0)的焦点,
F(0,
),
∵|FA|=c,
∴a2+
=c2①
抛物线的准线方程为y=-
由
得x=±
,
=2c②,
c2=2a2,
∵c2=a2+b2,
∴a=b,
∴双曲线的渐近线方程为:y=±x,
故答案为:y=±x.
∴A(a,0),
∵F为抛物线x2=2py(p>0)的焦点,
F(0,
| p |
| 2 |
∵|FA|=c,
∴a2+
| p2 |
| 4 |
抛物线的准线方程为y=-
| p |
| 2 |
由
|
| a |
| 2b |
| 4b2+p 2 |
| a |
| b |
| 4b2+p 2 |
c2=2a2,
∵c2=a2+b2,
∴a=b,
∴双曲线的渐近线方程为:y=±x,
故答案为:y=±x.
点评:熟练掌握圆锥曲线的图象与性质是解题的关键.

练习册系列答案
 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目
若二项式(2x+
)7的展开式中
的系数是84,则实数a=( )
| a |
| x |
| 1 |
| x3 |
| A、2 | ||||
B、
| ||||
| C、1 | ||||
D、
|
执行如图所示的程序框图,若输入的x,t均为2,则输出的S=( )


| A、4 | B、5 | C、6 | D、7 |
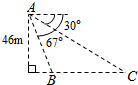 如图,从气球A上测得正前方的河流的两岸B,C的俯角分别为67°,30°,此时气球的高是46m,则河流的宽度BC约等于
如图,从气球A上测得正前方的河流的两岸B,C的俯角分别为67°,30°,此时气球的高是46m,则河流的宽度BC约等于