题目内容
在正四棱柱ABCD-A′B′C′D′中,AB=1,A′A=2,则AC′与BC所成角的余弦值是( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
考点:异面直线及其所成的角
专题:空间角
分析:以D为原点,DA为x轴,DC为y轴,DD1为z轴,建立空间直角坐标系,利用向量法能求出AC′与BC所成角的余弦值.
解答:
解: 以D为原点,DA为x轴,DC为y轴,DD1为z轴,
以D为原点,DA为x轴,DC为y轴,DD1为z轴,
建立空间直角坐标系,
由已知得A(1,0,0),C′(0,1,2),
B(1,1,0),C(0,1,0),
=(-1,1,2),
=(-1,0,0),
cos<
,
>=
=
.
∴AC′与BC所成角的余弦值是
.
故选:B.
 以D为原点,DA为x轴,DC为y轴,DD1为z轴,
以D为原点,DA为x轴,DC为y轴,DD1为z轴,建立空间直角坐标系,
由已知得A(1,0,0),C′(0,1,2),
B(1,1,0),C(0,1,0),
| AC′ |
| BC |
cos<
| AC′ |
| BC |
| 1 | ||
|
| ||
| 6 |
∴AC′与BC所成角的余弦值是
| ||
| 6 |
故选:B.
点评:本题考查空间角的求法,是基础题,解题时要认真审题,注意向量法的合理运用.

练习册系列答案
 名师点拨卷系列答案
名师点拨卷系列答案
相关题目
已知函数f(x)=
,若函数y=f(x+
)+n为奇函数,则实数n等于( )
| 1 |
| 4x+2 |
| 1 |
| 2 |
A、
| ||
| B、0 | ||
C、-
| ||
D、-
|
双曲线x2-y2=2的离心率是( )
| A、1 | ||
B、
| ||
| C、2 | ||
D、2
|
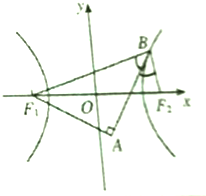 如图,F1、F2分别是双曲线x2-y2=1的左右焦点,点A的坐标是(
如图,F1、F2分别是双曲线x2-y2=1的左右焦点,点A的坐标是(