Question

已知实数a＞0，函数f（x）=

x(x-a)，(x≥0) - 9 40 x(x-a)，(x＜0)

（1）若函数f（x）在区间（-b，b）（b＞0）上存在最小值，求b的取值范围
（2）对于函数f（x），若存在区间[m，n]（n＞m），使{y|y=f（x），x∈[m，n]}=[m，n]，求a的取值范围，并写出满足条件的所有区间[m，n]．

Answer 1

考点：分段函数的应用,函数的最值及其几何意义

专题：计算题,数形结合,函数的性质及应用

分析：（1）画出函数f（x）的图象，由图象可得，函数f（x）在区间（-b，b）（b＞0）上存在最小值，最小值为

a

2

•（

a

2

-a）=-

a2

4

，令f（x）=-

a2

4

（x＜0），求出x，即可得到b的范围；
（2）画出直线y=x，求出交点，通过图象观察，当x＜0时，递增，再由x＞0的最小值，解不等式a-

40

9

≤-

a2

4

，即可得到a的范围，进而区间[m，n]．

解答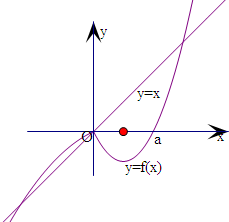： 解：（1）画出函数f（x）的图象，由图象可得，
函数f（x）在区间（-b，b）（b＞0）上存在最小值，
则最小值为

a

2

•（

a

2

-a）=-

a2

4

，令-

9

40

x（x-a）=-

a2

4

（x＜0），
解得x=-

2a

3

，即有

a

2

＜b≤

2a

3

；
（2）当区间[m，n]⊆（-∞，0），即为增区间，
由-

9

40

x（x-a）=x，可得x=0，或a-

40

9

，
由a-

40

9

＜0，可得0＜a＜

40

9

．
则区间m，n]为[a-

40

9

，0]，
再由x（x-a）=x，解得x=0或a+1，
由a-

40

9

≤-

a2

4

，解得-

20

3

≤a≤

8

3

．但a＞0，则有0＜a≤

8

3

．
则区间[m，n]为[a-

40

9

，a+1]．
综上可得a的范围是0＜a＜

40

9

，区间为[a-

40

9

，0]，[a-

40

9

，a+1]．

点评：本题考查分段函数的运用，考查函数的单调性的运用，考查数形结合的思想方法，考查运算能力，属于中档题．