题目内容
双曲线x2-y2=2的离心率是( )
| A、1 | ||
B、
| ||
| C、2 | ||
D、2
|
考点:双曲线的简单性质
专题:计算题,圆锥曲线的定义、性质与方程
分析:将双曲线方程化为标准方程,求出a,b,c,再由离心率公式计算即可得到.
解答:
解:双曲线x2-y2=2即为
-
=1,
则a=
,b=
,c=2,
即有e=
=
.
故选B.
| x2 |
| 2 |
| y2 |
| 2 |
则a=
| 2 |
| 2 |
即有e=
| c |
| a |
| 2 |
故选B.
点评:本题考查双曲线的方程和性质,考查离心率的求法,考查运算能力,属于基础题.

练习册系列答案
相关题目
已知x1,x2是方程x2-(k-2)+(k2+3k+5)=0(k∈R)的两个实根,则x12+x22的最大值为( )
| A、18 | ||
| B、19 | ||
C、5
| ||
| D、不存在 |
在正四棱柱ABCD-A′B′C′D′中,AB=1,A′A=2,则AC′与BC所成角的余弦值是( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
若已知两个变量x 和y 之间具有线性相关系,4 次试验的观测数据如下:
经计算得回归方程
=bx+a系数b=0.7,则a等于( )
| x | 3 | 4 | 5 | 6 |
| y | 2.5 | 3 | 4 | 4.5 |
| ∧ |
| y |
| A、0.34 | B、0.35 |
| C、0.45 | D、0.44 |

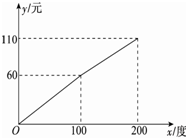 某供电公司为了合理分配电力,采用分段计算电费政策,月用电量x(度)与相应电费y(元)之间的函数关系的图象如图所示.
某供电公司为了合理分配电力,采用分段计算电费政策,月用电量x(度)与相应电费y(元)之间的函数关系的图象如图所示. 函数y=f(x)(x∈R)的图象如右图所示,下列说法正确的有
函数y=f(x)(x∈R)的图象如右图所示,下列说法正确的有