题目内容
为了某种需要，某班课外活动经常举行一种叫“电脑闯关比赛”的活动，在一次“电脑闯关比赛”中，A、B两位同学在同等的条件下进行闯关赛，为了预测他们的闯关能力，现随机抽取这两个同学以往一起闯关比赛的结果为：（a，b），（a，
），（a，b），（
，b），（
，
），（a，b），（a，b），（a，b），（
，b），（a，
），（
，
），（a，b），（a，
），（
，b），（a，b）其中a，
分别表示A同学闯关成功和失败；b，
分别表示B同学闯关成功和失败．
（1）若闯关成功，则给该同学记2分，否则记0分，试计算A、B两位同学闯关成绩的平均数和方差，并比较A、B两位同学的闯关能力；
（2）现A、B两位同学只进行一次对抗赛，试估算至少有一位同学闯关成功的概率．
. |
| b |
. |
| a |
. |
| a |
. |
| b |
. |
| a |
. |
| b |
. |
| a |
. |
| b |
. |
| b |
. |
| a |
. |
| a |
. |
| b |
（1）若闯关成功，则给该同学记2分，否则记0分，试计算A、B两位同学闯关成绩的平均数和方差，并比较A、B两位同学的闯关能力；
（2）现A、B两位同学只进行一次对抗赛，试估算至少有一位同学闯关成功的概率．
考点：相互独立事件的概率乘法公式,极差、方差与标准差
专题：综合题,概率与统计
分析：（Ⅰ）分别求出甲乙的闯关成绩，再根据平均数和方差公式计算平均数，方差，最后比较即可．
（Ⅱ）找15个结果中，找到恰有闯关成功的结果是7个，求出频率，将频率视为概率，问题得以解决．
（Ⅱ）找15个结果中，找到恰有闯关成功的结果是7个，求出频率，将频率视为概率，问题得以解决．
解答：
解：（Ⅰ）A同学闯关成绩的成绩为2，2，2，0，0，2，2，2，0，2，0，2，2，0，2，
则
=
，S甲2=
；
B同学闯关成绩的成绩为2，0，2，2，0，2，2，0，2，0，0，2，0，2，2，则
=
，S乙2=
．
因为
＞
，S甲2＜S乙2
所以甲的研发水平高于乙的研发水平．
（Ⅱ）记E={恰有一位同学闯关成功}，在所抽到的15个结果中，
恰有一位同学闯关成功的结果是（a，
），（
，b），（a，
），（
，b），（a，
），（a，
），（
，b）共7个，
故事件E发生的频率为
，
将频率视为概率，即恰有一位同学闯关成功的概率为P（E）=
．
则
. |
| x甲 |
| 4 |
| 3 |
| 8 |
| 9 |
B同学闯关成绩的成绩为2，0，2，2，0，2，2，0，2，0，0，2，0，2，2，则
. |
| x乙 |
| 6 |
| 5 |
| 24 |
| 25 |
因为
. |
| x甲 |
. |
| x乙 |
所以甲的研发水平高于乙的研发水平．
（Ⅱ）记E={恰有一位同学闯关成功}，在所抽到的15个结果中，
恰有一位同学闯关成功的结果是（a，
. |
| b |
. |
| a |
. |
| b |
. |
| a |
. |
| b |
. |
| b |
. |
| a |
故事件E发生的频率为
| 7 |
| 15 |
将频率视为概率，即恰有一位同学闯关成功的概率为P（E）=
| 7 |
| 15 |
点评：本题主要考查了平均数方差和用频率表示概率，培养的学生的运算能力．
练习册系列答案
阅读快车系列答案
相关题目
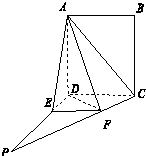如图，四边形ABCD为正方形，PD⊥平面ABCD，PD=AD，AF⊥PC于点F，FE∥CD交PD于点E．